freeCodeCamp/curriculum/challenges/ukrainian/10-coding-interview-prep/project-euler/problem-256-tatami-free-rooms.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f46c1000cf542c50ff7e	Завдання 256: Кімнати без татамі	5	301904	problem-256-tatami-free-rooms

--description--

Татамі - це прямокутні мати, якими повністю покривають підлогу кімнати, таким чином, що вони не перекривають один одного.

Припустимо, що єдиний можливий вид татамі має розміри 1×2, очевидно, що на розмір і форму кімнати накладаються деякі обмеження, щоб підлогу кімнати можна було покрити повністю.

У цьому завданні ми розглядаємо тільки кімнати прямокутної форми з цілими розмірами a, b і парним розміром s = a \times b. Використовуємо термін "розмір", щоб позначити площу поверхні підлоги кімнати і, без втрати узагальненості, додамо вимогу a ≤ b.

При укладанні татамі є одне правило, якого необхідно дотримуватися: не повинно бути жодної такої точки, де б стикалося чотирьох різних мати. Наприклад, розглянемо два варіанти покриття підлоги кімнати 4×4:

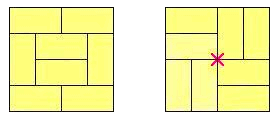
Варіант розташування ліворуч допустимий, в той час, як варіант праворуч — ні: червоний символ "X" усередині позначає точку стику чотирьох матів татамі.

Через це правило, кімнати з парними розмірами не завжди можна покрити підлогу татамі: ми називаємо їх кімнатами без татамі. Також, визначимо T(s) як число кімнат без татамі розміром s.

Найменша кімната без татамі має розмір s = 70 та розміри 7×10. Підлоги всіх інших кімнат розміром s = 70 можна покрити татамі; розміри таких кімнат: 1×70, 2×35 та 5×14. Отже, T(70) = 1.

Аналогічно, ми можемо переконатися в тому, що T(1320) = 5, оскільки існує лише 5 кімнат без татамі розміром s = 1320: 20×66, 22×60, 24×55, 30×44 та 33×40. Фактично, s = 1320 є найменшим розміром s кімнати, для якої T(s) = 5.

Знайдіть найменший розмір кімнати s, при якому T(s) = 200.

--hints--

tatamiFreeRooms() має повернути 85765680.

assert.strictEqual(tatamiFreeRooms(), 85765680);

--seed--

--seed-contents--

function tatamiFreeRooms() {

  return true;
}

tatamiFreeRooms();

--solutions--

// solution required