freeCodeCamp/curriculum/challenges/ukrainian/10-coding-interview-prep/project-euler/problem-287-quadtree-encoding-a-simple-compression-algorithm.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f48b1000cf542c50ff9e	Проблема 287: Кодування Дерева квадратів (простий алгоритм стиснення)	5	301938	problem-287-quadtree-encoding-a-simple-compression-algorithm

--description--

Кодування дерева квадратів дозволяє описати чорно-біле зображення 2^N×2^N як послідовність бітів (0 та 1). Ці послідовності читаються зліва направо - так:

• перший біт укладається з повною базою 2^N×2^N регіону;
• "0" показує розділення:
  • поточна площа 2^n×2^n поділена на 4 півплощі виміру 2^{n - 1}×2^{n - 1},
  • наступні біти містять опис верхнього лівого верхнього лівого і правого верхнього та нижнього правого підплощ - в такому порядку;
• "10" вказує на те, що поточна площа містить лише чорні пікселі;
• "11" вказує, що поточна площа містить лише білі пікселі.

Розглянемо зображення 4×4 (кольорові марки означають місце, де може відбутися розділ):

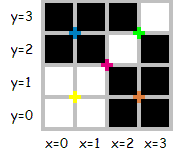
Це зображення може бути описано декількома послідовностями, Наприклад,"001010101001011111011010101010", довжиною 30, або "0100101111101110", довжиною 16, якою є мінімальна послідовність для цього зображення.

Для позитивного цілого $N$визначте D_N як 2^N×2^N зображення з наступною кольоровою схемою:

• піксель з координатами x = 0, y = 0 відповідає нижньому лівому пікселю,
• якщо {(x - 2^{N - 1})}^2 + {(y - 2^{N - 1})}^2 ≤ 2^{2N - 2} тоді, піксель чорний,
• інакше піксель - білий.

Яка довжина мінімальної послідовності, що описує D_{24}?

--hints--

quadtreeEncoding() має повернути 313135496.

assert.strictEqual(quadtreeEncoding(), 313135496);

--seed--

--seed-contents--

function quadtreeEncoding() {

  return true;
}

quadtreeEncoding();

--solutions--

// solution required