2.5 KiB
2.5 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f49f1000cf542c50ffb1 | Проблема 306: Гра з паперовими стрічками | 5 | 301960 | problem-306-paper-strip-game |
--description--
Наведена нижче гра є класичним прикладом Теорії комбінаторіальної гри:
Двоє гравців починають з смужки n білих квадратів і почергово ходять. Під час кожного ходу, гравець вибирає два суміжних білих квадратики і розмальовує їх у чорний колір. Перший гравець, який не може зробити хід - програє.
n = 1: Немає дійсних кроків, тому перший гравець автоматично програє.n = 2: Лише один дійсний крок, після якого другий гравець програє.n = 3: два дійсні кроки, але обидва залишають положення, де другий гравець програє.n = 4: Є три дійсні кроки для першого гравця; який може виграти гру замалювавши два середніх квадрати.n = 5: чотири дійсні кроки для першого гравця (показано нижче червоним кольором); але незважаючи на те, що буде робити гравець, другий гравець (синій) виграє.
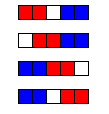
Тому за 1 ≤ n ≤ 5, є 3 значення n, для яких перший гравець може прийти до виграшу.
Тому за 1 ≤ n ≤ 50, є 40 значень n, для яких перший гравець може прийти до виграшу.
Що за 1 ≤ 1\\,000\\,000, скільки значень n для чого перший гравець може виграти?
--hints--
paperStripGame() має повернути 852938.
assert.strictEqual(paperStripGame(), 852938);
--seed--
--seed-contents--
function paperStripGame() {
return true;
}
paperStripGame();
--solutions--
// solution required