1.9 KiB
1.9 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f5081000cf542c510019 | Завдання 411: Шлях вгору | 5 | 302080 | problem-411-uphill-paths |
--description--
Нехай n — це додатне ціле число. Припустимо, що є такі точки з координатами (x, y) = (2^i\bmod n, 3^i\bmod n) для 0 ≤ i ≤ 2n. Вважатимемо точки з однаковими координатами, як одну й ту саму точку.
Потрібно створити шлях від (0, 0) до (n, n) таким чином, щоб координати x та y не зменшувалися.
Нехай S(n) — це максимальна кількість точок, через які може проходити шлях.
Наприклад, якщо n = 22, то є 11 точок, а допустимий шлях може проходити щонайбільше через 5 точок. Таким чином, S(22) = 5. Ілюстрація цього прикладу подана нижче, на ній можна побачити зразок оптимального шляху:
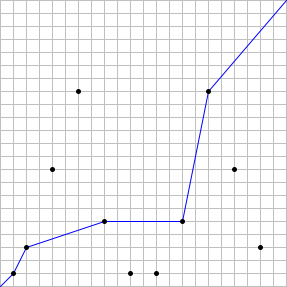
Також можна перевірити, що S(123) = 14, а S(10\\,000) = 48.
Знайдіть \sum S(k^5) для 1 ≤ k ≤ 30.
--hints--
uphillPaths() має повернути 9936352.
assert.strictEqual(uphillPaths(), 9936352);
--seed--
--seed-contents--
function uphillPaths() {
return true;
}
uphillPaths();
--solutions--
// solution required