3.6 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f51f1000cf542c510031 | Завдання 434: Незмінні графіки | 5 | 302105 | problem-434-rigid-graphs |
--description--
Нагадаємо, що графік це набір вершин та кутів, які їх з'єднують. Дві вершини, з'єднані кутом, називаються прилеглими.
Графіки можуть бути вбудовані в Евклідів простір через спрягання кожної вершини з точкою в Евклідовому просторі.
Гнучким називають графік, в якому можна постійно рухати однією або й більше вершинами таким чином, щоб відстань між принаймні двома несуміжними вершинами змінювалась, в той час як дистанція між кожною парою суміжних вершин постійно залишалась без змін.
Незмінним називають графік, який не являється гнучким.
Неформально графік є стійким, якщо, замінивши вершини повністю обертовими петлями, а ребра стержнями, які є еластичними та не розгинаються, жодна частина графіка не може бути переміщена незалежно від решти графіка.
Табличні графіки, які вбудовані в евклідову площину, не є незмінними, як показує наступний рисунок:
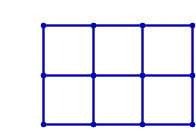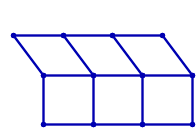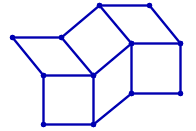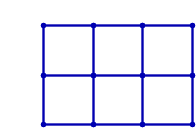
Однак їх можна зробити незмінними, додавши діагональні краї до комірок. Наприклад, для табличного графіка 2х3 існує 19 способів зробити графік незмінним:

Зверніть увагу, що для цілей цього завдання ми не розглядаємо зміну орієнтації діагонального ребра або додавання обох діагональних ребер до комірки як інший спосіб зробити незмінний табличний графік.
Нехай R(m, n) буде кількістю способів створити табличний незмінний графік m × n.
Наприклад: R(2, 3) = 19 таR(5, 5) = 23\\,679\\,901.
Визначимо S(N) як \суму R(i, j) для 1 ≤ i, j ≤ N.
Наприклад: S(5) = 25\\,021\\,721.
Знайдіть S(100), дайте відповідь модулем 1\\,000\\,000\\,033.
--hints--
rigidGraphs() має видати 863253606.
assert.strictEqual(rigidGraphs(), 863253606);
--seed--
--seed-contents--
function rigidGraphs() {
return true;
}
rigidGraphs();
--solutions--
// solution required