3.0 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f5381000cf542c51004b | Завдання 460: Мураха на ходу | 5 | 302135 | problem-460-an-ant-on-the-move |
--description--
На Евклідовій площині мураха подорожує з точки A(0, 1) у точку B(d, 1) за ціле число d.
На кожному кроці, мураха в точці (x_0, y_0) обирає одну з точок решітки (x_1, y_1), що задовольняє вираз x_1 ≥ 0 та y_1 ≥ 1, для того, щоб перейти в точку (x_1, y_1) з постійною швидкістю v. Значення v залежить від y_0 та y_1 наступним чином:
- Якщо
y_0 = y_1, значенняvдорівнюєy_0. - Якщо
y_0 ≠ y_1, значенняvдорівнює\frac{y_1 - y_0}{\ln y_1 - \ln y_0}.
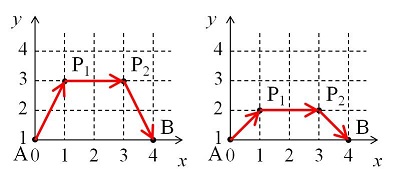
Зображення ліворуч показує один із можливих шляхів коли d = 4. Спочатку мураха рушає з A(0, 1) у P_1(1, 3) зі швидкістю \frac{3 - 1}{\ln 3 - \ln 1} ≈ 1.8205. Тоді необхідний для цього час - це \frac{\sqrt{5}}{1.820} ≈ 1.2283.
Із точки P_1(1, 3) у точку P_2(3, 3) мураха подорожує зі швидкістю 3, тому необхідний час буде \frac{2}{3} ≈ 0.6667. Із точки P_2(3, 3) у точку B(4, 1) мураха подорожує зі швидкістю \frac{1 - 3}{\ln 1 - \ln 3} ≈ 1.8205 тому необхідний час буде \frac{\sqrt{5}}{1.8205} ≈ 1.2283.
Таким чином, загальний необхідний час буде 1.2283 + 0.6667 + 1.2283 = 3.1233.
Зображення праворуч демонструє інший шлях. Загальний необхідний час вираховується як 0.98026 + 1 + 0.98026 = 2.96052. Можна зробити висновок, що це найшвидший шлях для d = 4.
Нехай F(d) буде загальним необхідним часом, якщо мураха обирає найшвидший шлях. Наприклад, F(4) ≈ 2.960\\,516\\,287. Можемо перевірити, що F(10) ≈ 4.668\\,187\\,834 та F(100) ≈ 9.217\\,221\\,972.
Знайдіть F(10\\,000). Дайте відповідь, округлену до 9 знаків після коми.
--hints--
antOnTheMove() повинна повернути 18.420738199.
assert.strictEqual(antOnTheMove(), 18.420738199);
--seed--
--seed-contents--
function antOnTheMove() {
return true;
}
antOnTheMove();
--solutions--
// solution required