1.3 KiB
1.3 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f3f61000cf542c50ff09 | 问题 138:特殊的等腰三角形 | 5 | 301766 | problem-138-special-isosceles-triangles |
--description--
考虑一个底边长为 $b = 16$,腰长为 L = 17 的等腰三角形。
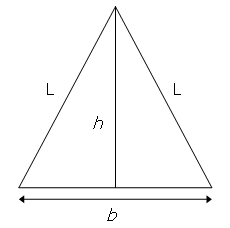
使用毕达哥拉斯定理,可以求出三角形的高为 $h = \sqrt{{17}^2 − 8^2} = 15$,恰好比底边长度小 1。
当等腰三角形底边长为 $b = 272$,腰长为 L = 305 时,计算可得高为 $h = 273$,恰好比底边长度大 1,并且这是第二小的满足性质 h = b ± 1 的等腰三角形。
找到最小的 12 个满足 h = b ± 1 且 $b$,L 均为正整数的等腰三角形,求 $\sum{L}$。
--hints--
isoscelesTriangles() 应该返回 1118049290473932。
assert.strictEqual(isoscelesTriangles(), 1118049290473932);
--seed--
--seed-contents--
function isoscelesTriangles() {
return true;
}
isoscelesTriangles();
--solutions--
// solution required