1.5 KiB
1.5 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f46e1000cf542c50ff80 | 問題 257: 角の二等分線 | 5 | 301905 | problem-257-angular-bisectors |
--description--
整数の辺長を持つ三角形 ABC が与えられ、辺は a ≤ b ≤ c です (AB = c, BC = a, AC = b)。
三角形の角の二等分線は、点 E, F, G で辺と交わります (下図参照)。
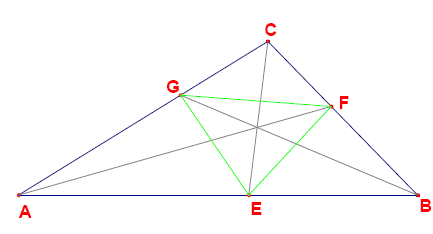
線分 EF, EG, FG は、ABC を 4 つの小さな三角形 AEG, BFE, CGF, EFG に分割します。 この 4 つの三角形のそれぞれについて、比率 \frac{\text{面積}(ABC)}{\text{面積}(\text{部分三角形})} が有理数であることを証明できます。 しかし、これらの比率の一部またはすべてが整数である三角形が存在します。
周長が 100\\,000\\,000 以下で、比率 \frac{\text{面積}(ABC)}{\text{面積}(AEG)} が整数である三角形 ABC はいくつ存在しますか。
--hints--
angularBisectors() は 139012411 を返す必要があります。
assert.strictEqual(angularBisectors(), 139012411);
--seed--
--seed-contents--
function angularBisectors() {
return true;
}
angularBisectors();
--solutions--
// solution required