1.6 KiB
1.6 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f48d1000cf542c50ffa0 | 問題 289: オイラー閉路 | 5 | 301940 | problem-289-eulerian-cycles |
--description--
点 (x, y), (x, y + 1), (x + 1, y), (x + 1, y + 1) を通過する円を C(x,y) とします。
正の整数 m, n に対し、m·n の円 { C(x,y): 0 ≤ x < m, 0 ≤ y < n, x と y は整数 } からなる図形を $E (m,n) とします。
E(m,n) 上のオイラー閉路は、各弧をちょうど 1 回ずつ通る閉路です。 E(m,n) 上にはそのような経路が数多くありますが、ここではそれ自体と交差しないもののみに注目します。交差しない経路とは、格子点でそれ自体に触れるだけであり、それ自体と決して交わらない経路です。
下の画像は、E(3,3) と、交差しないオイラー経路の例です。
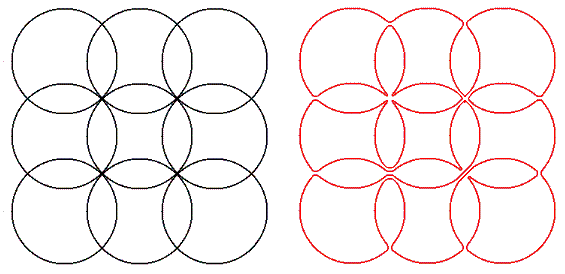
E(m,n) 上の交差しないオイラー経路の数を L(m,n) とします。 例えば、L(1,2) = 2, L(2,2) = 37, L(3,3) = 104290 です。
L(6,10)\bmod {10}^{10} を求めなさい。
--hints--
eulerianCycles() は 6567944538 を返す必要があります。
assert.strictEqual(eulerianCycles(), 6567944538);
--seed--
--seed-contents--
function eulerianCycles() {
return true;
}
eulerianCycles();
--solutions--
// solution required