Files

camperbot 43a2a0a395 chore(i18n,learn): processed translations (#44866 )

2022-01-23 00:08:20 +09:00

2.4 KiB

Raw Blame History

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f4d91000cf542c50ffeb	問題 363: ベジェ曲線	5	302024	problem-363-bzier-curves

--description--

三次ベジェ曲線は P_0, P_1, P_2, P_3 の 4 点で定義されます。

この曲線は次のように形成されます。

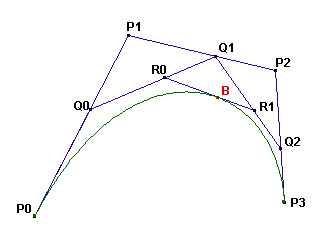
線分 P_0P_1, P_1P_2, P_2P_3 上に点 Q_0,$Q_1$, Q_2 が、区間 [0,1] 内の t について \frac{P_0Q_0}{P_0P_1} = \frac{P_1Q_1}{P_1P_2} = \frac{P_2Q_2}{P_2P_3} = t となるように描かれます。

線分 Q_0Q_1 と Q_1Q_2 上に点 R_0 と R_1 が、上と同じ t の値について \frac{Q_0R_0}{Q_0Q_1} = \frac{Q_1R_1}{Q_1Q_2} = t となるように描かれます。

線分 R_0R_1 上に点 B が、上と同じ t の値について \frac{R_0B}{R_0R_1} = t となるように描かれます。

点 P_0, P_1, P_2, P_3 によって定義されるベジェ曲線は、Q_0 が線分 P_0P_1 上の考えられるすべての位置を取る際の B の軌跡です。 (すべての点において t の値が同じであることに注意してください。)

作成された図を見れば分かるとおり、ベジェ曲線は P_0 において線分 P_0P_1 と接し、そして P_3 において線分 P_2P_3 と接しています。

P_0 = (1, 0), P_1 = (1, v), P_2 = (v. 1), P_3 = (0, 1) で定義される三次ベジェ曲線は、4 分の 1 円弧に近付けるために使用されます。値 v > 0 は、直線 OP_0, OP_3 と曲線で囲まれた部分の面積が \frac{π}{4} (4 分の 1 円弧) と等しくなるように選択されます。

曲線の長さは 4 分の 1 円弧の長さと何パーセント異なりますか。つまり、L を曲線の長さとすると、100 × \displaystyle\frac{L − \frac{π}{2}}{\frac{π}{2}} を計算します。回答は、四捨五入して小数第 10 位まで示すこと。

--hints--

bezierCurves() は 0.0000372091 を返す必要があります。

assert.strictEqual(bezierCurves(), 0.0000372091);

--seed--

--seed-contents--

function bezierCurves() {

  return true;
}

bezierCurves();

--solutions--

// solution required

2.4 KiB Raw Blame History Unescape Escape