Files

camperbot 43a2a0a395 chore(i18n,learn): processed translations (#44866 )

2022-01-23 00:08:20 +09:00

1.7 KiB

Raw Blame History

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f5241000cf542c510037	問題 440: 最大公約数とタイル貼り	5	302112	problem-440-gcd-and-tiling

--description--

1 × 2 のタイル、または下図のように 1 桁の 10 進数が書かれた 1 × 1 のタイルを、長さ$n$、高さ 1 の板全体に貼ります。

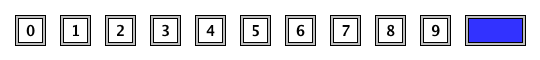
1 桁の 10 進数が書かれた 1 × 1 のブロックと、1 x 2 のブロック

例えば、n = 8 のときに板にタイルを貼る方法をいくつか示します。

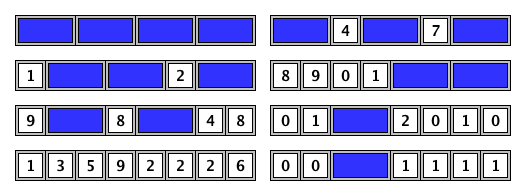
上述の長さ n の板にタイルを貼る方法の数を T(n) とします。

例えば、T(1) = 10, T(2) = 101 です。

1 ≤ a, b, c ≤ L のとき、三重和 \sum_{a, b, c} gcd(T(c^a), T(c^b)) を S(L) とします。

例えば、次のようになります。

\begin{align} & S(2) = 10\\,444 \\\\ & S(3) = 1\\,292\\,115\\,238\\,446\\,807\\,016\\,106\\,539\\,989 \\\\ & S(4)\bmod 987\\,898\\,789 = 670\\,616\\,280. \end{align}

S(2000)\bmod 987\\,898\\,789 を求めなさい。

--hints--

gcdAndTiling() は 970746056 を返す必要があります。

assert.strictEqual(gcdAndTiling(), 970746056);

--seed--

--seed-contents--

function gcdAndTiling() {

  return true;
}

gcdAndTiling();

--solutions--

// solution required

1.7 KiB Raw Blame History Unescape Escape