* fix: improve Project Euler descriptions and test case Improve formatting of Project Euler test descriptions. Also add poker hands array and new test case for problem 54 * feat: add typeof tests and gave functions proper names for first 100 challenges * fix: continue fixing test descriptions and adding "before test" sections * fix: address review comments * fix: adjust grids in 18 and 67 and fix some text that reference files rather than the given arrays * fix: implement bug fixes and improvements from review * fix: remove console.log statements from seed and solution
2.1 KiB
2.1 KiB
id, challengeType, title, forumTopicId
| id | challengeType | title | forumTopicId |
|---|---|---|---|
| 5900f3c71000cf542c50feda | 5 | Problem 91: Right triangles with integer coordinates | 302208 |
Description
The points P (x1, y1) and Q (x2, y2) are plotted at integer co-ordinates and are joined to the origin, O(0,0), to form ΔOPQ.
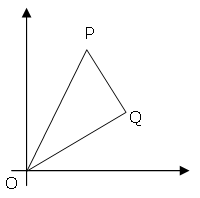
There are exactly fourteen triangles containing a right angle that can be formed when each co-ordinate lies between 0 and 2 inclusive; that is, 0 ≤ x1, y1, x2, y2 ≤ 2.
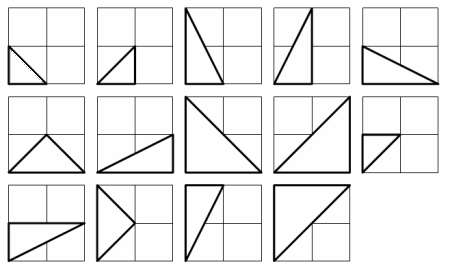
Given that 0 ≤ x1, y1, x2, y2 ≤ 50, how many right triangles can be formed?
Instructions
Tests
tests:
- text: <code>rightTrianglesIntCoords()</code> should return a number.
testString: assert(typeof rightTrianglesIntCoords() === 'number');
- text: <code>rightTrianglesIntCoords()</code> should return 14234.
testString: assert.strictEqual(rightTrianglesIntCoords(), 14234);
Challenge Seed
function rightTrianglesIntCoords() {
// Good luck!
return true;
}
rightTrianglesIntCoords();
Solution
// solution required