2.2 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4031000cf542c50ff15 | Problema 150: Procura de uma matriz triangular para um subtriângulo com a soma mínima | 5 | 301781 | problem-150-searching-a-triangular-array-for-a-sub-triangle-having-minimum-sum |
--description--
Em uma matriz triangular de números inteiros positivos e negativos, queremos encontrar um subtriângulo onde a soma dos números nele contidos seja a menor possível.
No exemplo abaixo, pode ser facilmente verificado que o triângulo marcado satisfaz esta condição tendo uma soma de -42.
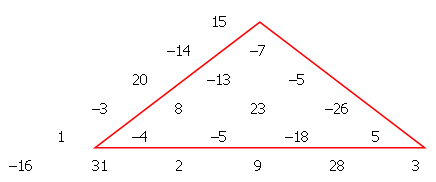
Queremos fazer uma matriz triangular desse tipo com mil fileiras. Então, geramos 500500 números pseudoaleatórios s_k no intervalo ±2^{19}, usando um tipo de gerador de número aleatório (conhecido como gerador congruente linear), da seguinte forma:
\begin{align} t := & \\ 0\\\\ \text{for}\\ & k = 1\\ \text{up to}\\ k = 500500:\\\\ & t := (615949 × t + 797807)\\ \text{modulo}\\ 2^{20}\\\\ & s_k := t − 219\\\\ \end{align}
Assim: s_1 = 273519, s_2 = −153582, s_3 = 450905 e assim por diante.
Nossa matriz triangular é então formada usando os pseudonúmeros aleatórios, ou seja:
s_1 \\\\ s_2\\;s_3 \\\\ s_4\\; s_5\\; s_6 \\\\ s_7\\; s_8\\; s_9\\; s_{10} \\\\ \ldots
Os subtriângulos podem começar em qualquer elemento da matriz e se estender até onde quisermos (pegando os dois elementos diretamente abaixo dele na próxima fileira, sendo os três elementos diretamente abaixo da linha depois disso e assim por diante).
A "soma de um subtriângulo" é definida como a soma de todos os elementos que o contêm.
Encontre o subtriângulo de menor soma de elementos possível.
--hints--
smallestSubTriangleSum() deve retornar -271248680.
assert.strictEqual(smallestSubTriangleSum(), -271248680);
--seed--
--seed-contents--
function smallestSubTriangleSum() {
return true;
}
smallestSubTriangleSum();
--solutions--
// solution required