Files

gikf 32fac23a2d fix(curriculum): clean-up Project Euler 161-180 (#42782 )

* fix: clean-up Project Euler 161-180

* fix: corrections from review

Co-authored-by: Tom <20648924+moT01@users.noreply.github.com>

Co-authored-by: Tom <20648924+moT01@users.noreply.github.com>

2021-07-12 16:19:03 +02:00

1.6 KiB

Raw Blame History

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f41a1000cf542c50ff2d	Problem 174: Counting the number of "hollow" square laminae that can form one, two, three, ... distinct arrangements	5	301809	problem-174-counting-the-number-of-hollow-square-laminae-that-can-form-one-two-three-----distinct-arrangements

--description--

We shall define a square lamina to be a square outline with a square "hole" so that the shape possesses vertical and horizontal symmetry.

Given eight tiles it is possible to form a lamina in only one way: 3x3 square with a 1x1 hole in the middle. However, using thirty-two tiles it is possible to form two distinct laminae.

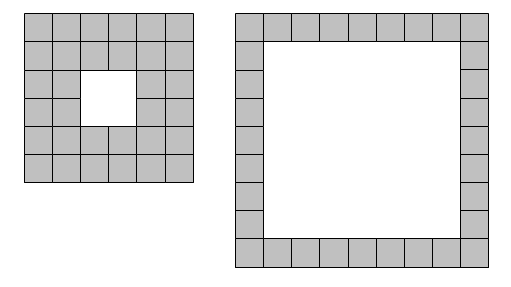
two square lamina with holes 2x2 and 7x7

If t represents the number of tiles used, we shall say that t = 8 is type L(1) and t = 32 is type L(2).

Let N(n) be the number of t ≤ 1000000 such that t is type L(n); for example, N(15) = 832.

What is \sum N(n) for 1 ≤ n ≤ 10?

--hints--

hollowSquareLaminaeDistinctArrangements() should return 209566.

assert.strictEqual(hollowSquareLaminaeDistinctArrangements(), 209566);

--seed--

--seed-contents--

function hollowSquareLaminaeDistinctArrangements() {

  return true;
}

hollowSquareLaminaeDistinctArrangements();

--solutions--

// solution required

1.6 KiB Raw Blame History