Files

gikf 67de105117 fix(curriculum): clean-up Project Euler 241-260 (#42879 )

* fix: clean-up Project Euler 241-260

* fix: typo

* Update curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-255-rounded-square-roots.md

Co-authored-by: Tom <20648924+moT01@users.noreply.github.com>

2021-07-16 12:21:45 +02:00

1.7 KiB

Raw Blame History

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f4621000cf542c50ff75	Problem 246: Tangents to an ellipse	5	301893	problem-246-tangents-to-an-ellipse

--description--

A definition for an ellipse is:

Given a circle c with centre M and radius r and a point G such that d(G, M) < r, the locus of the points that are equidistant from c and G form an ellipse.

The construction of the points of the ellipse is shown below.

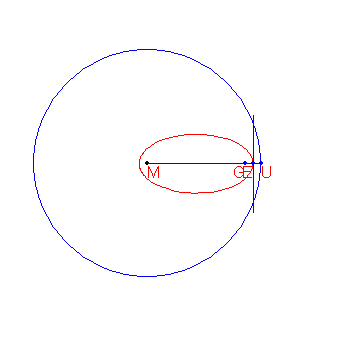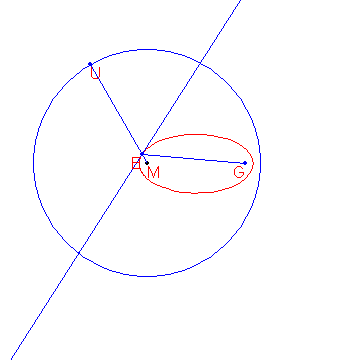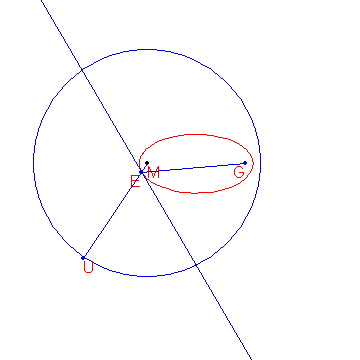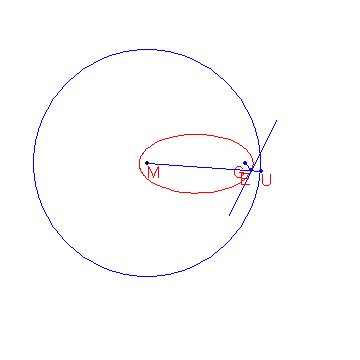
Given are the points M(-2000, 1500) and G(8000, 1500).

Given is also the circle c with centre M and radius 15\\,000.

The locus of the points that are equidistant from G and c form an ellipse e.

From a point P outside e the two tangents t_1 and t_2 to the ellipse are drawn.

Let the points where t_1 and t_2 touch the ellipse be R and S.

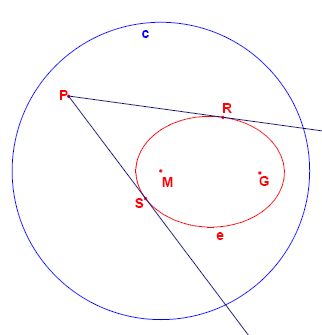
circle c with the centre M, radius 15000, and point P outsie of ellipse e; from point P two tangents t_1 and t_2 are drawn to the ellipse, with points touching ellipse are R and S

For how many lattice points P is angle RPS greater than 45°?

--hints--

tangentsToAnEllipse() should return 810834388.

assert.strictEqual(tangentsToAnEllipse(), 810834388);

--seed--

--seed-contents--

function tangentsToAnEllipse() {

  return true;
}

tangentsToAnEllipse();

--solutions--

// solution required

1.7 KiB Raw Blame History