* fix: clean-up Project Euler 301-320 * fix: corrections from review Co-authored-by: Tom <20648924+moT01@users.noreply.github.com> Co-authored-by: Tom <20648924+moT01@users.noreply.github.com>
1.4 KiB
1.4 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4a31000cf542c50ffb6 | Problem 311: Biclinic Integral Quadrilaterals | 5 | 301967 | problem-311-biclinic-integral-quadrilaterals |
--description--
ABCD is a convex, integer sided quadrilateral with 1 ≤ AB < BC < CD < AD.
BD has integer length. O is the midpoint of BD. AO has integer length.
We'll call ABCD a biclinic integral quadrilateral if AO = CO ≤ BO = DO.
For example, the following quadrilateral is a biclinic integral quadrilateral: AB = 19, BC = 29, CD = 37, AD = 43, BD = 48 and AO = CO = 23.
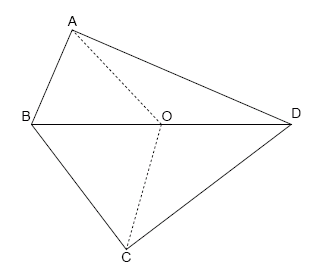
Let B(N) be the number of distinct biclinic integral quadrilaterals ABCD that satisfy {AB}^2 + {BC}^2 + {CD}^2 + {AD}^2 ≤ N. We can verify that B(10\\,000) = 49 and B(1\\,000\\,000) = 38239.
Find B(10\\,000\\,000\\,000).
--hints--
biclinicIntegralQuadrilaterals() should return 2466018557.
assert.strictEqual(biclinicIntegralQuadrilaterals(), 2466018557);
--seed--
--seed-contents--
function biclinicIntegralQuadrilaterals() {
return true;
}
biclinicIntegralQuadrilaterals();
--solutions--
// solution required