* fix: clean-up Project Euler 341-360 * fix: improve wording Co-authored-by: Sem Bauke <46919888+Sembauke@users.noreply.github.com> * fix: corrections from review Co-authored-by: Tom <20648924+moT01@users.noreply.github.com> Co-authored-by: Sem Bauke <46919888+Sembauke@users.noreply.github.com> Co-authored-by: Tom <20648924+moT01@users.noreply.github.com>
1.3 KiB
1.3 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4cf1000cf542c50ffe1 | Problem 354: Distances in a bee's honeycomb | 5 | 302014 | problem-354-distances-in-a-bees-honeycomb |
--description--
Consider a honey bee's honeycomb where each cell is a perfect regular hexagon with side length 1.
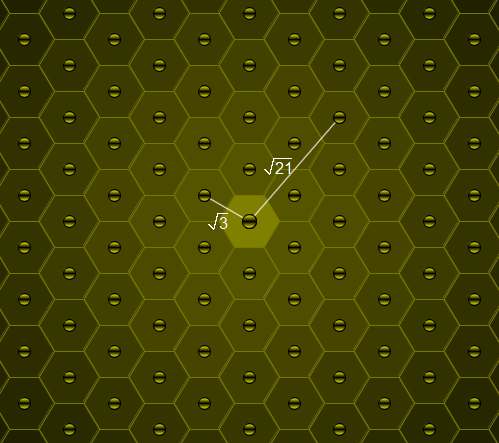
One particular cell is occupied by the queen bee. For a positive real number L, let B(L) count the cells with distance L from the queen bee cell (all distances are measured from centre to centre); you may assume that the honeycomb is large enough to accommodate for any distance we wish to consider.
For example, B(\sqrt{3}) = 6, B(\sqrt{21}) = 12 and B(111\\,111\\,111) = 54.
Find the number of L ≤ 5 \times {10}^{11} such that B(L) = 450.
--hints--
distancesInHoneycomb() should return 58065134.
assert.strictEqual(distancesInHoneycomb(), 58065134);
--seed--
--seed-contents--
function distancesInHoneycomb() {
return true;
}
distancesInHoneycomb();
--solutions--
// solution required