* fix: clean-up Project Euler 361-380 * fix: improve wording Co-authored-by: Sem Bauke <46919888+Sembauke@users.noreply.github.com> * fix: remove unnecessary paragraph * fix: corrections from review Co-authored-by: Tom <20648924+moT01@users.noreply.github.com> Co-authored-by: Sem Bauke <46919888+Sembauke@users.noreply.github.com> Co-authored-by: Tom <20648924+moT01@users.noreply.github.com>
1.3 KiB
1.3 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4d91000cf542c50ffea | Problem 364: Comfortable distance | 5 | 302025 | problem-364-comfortable-distance |
--description--
There are N seats in a row. N people come after each other to fill the seats according to the following rules:
- If there is any seat whose adjacent seat(s) are not occupied take such a seat.
- If there is no such seat and there is any seat for which only one adjacent seat is occupied take such a seat.
- Otherwise take one of the remaining available seats.
Let T(N) be the number of possibilities that N seats are occupied by N people with the given rules. The following figure shows T(4) = 8.
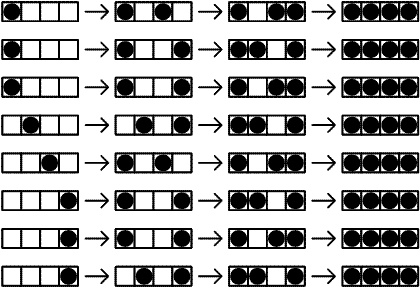
We can verify that T(10) = 61\\,632 and T(1\\,000)\bmod 100\\,000\\,007 = 47\\,255\\,094.
Find T(1\\,000\\,000)\bmod 100\\,000\\,007.
--hints--
comfortableDistance() should return 44855254.
assert.strictEqual(comfortableDistance(), 44855254);
--seed--
--seed-contents--
function comfortableDistance() {
return true;
}
comfortableDistance();
--solutions--
// solution required