freeCodeCamp/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-405-a-rectangular-tiling.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f5021000cf542c510014	Problem 405: A rectangular tiling	5	302073	problem-405-a-rectangular-tiling

--description--

We wish to tile a rectangle whose length is twice its width.

Let T(0) be the tiling consisting of a single rectangle.

For n > 0, let T(n) be obtained from T( n- 1) by replacing all tiles in the following manner:

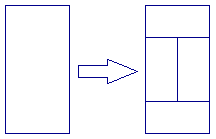
The following animation demonstrates the tilings T(n) for n from 0 to 5:

Let f(n) be the number of points where four tiles meet in T(n). For example, f(1) = 0, f(4) = 82 and f({10}^9)\bmod {17}^7 = 126\\,897\\,180.

Find f({10}^k) for k = {10}^{18}, give your answer modulo {17}^7.

--hints--

rectangularTiling() should return 237696125.

assert.strictEqual(rectangularTiling(), 237696125);

--seed--

--seed-contents--

function rectangularTiling() {

  return true;
}

rectangularTiling();

--solutions--

// solution required