2.2 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4971000cf542c50ffaa | Завдання 299: Три подібні трикутники | 5 | 301951 | problem-299-three-similar-triangles |
--description--
Визначено чотири точки з цілими координатами:
A(a, 0), B(b, 0), C(0, c) і D(0, d), з 0 < a < b і 0 < c < d.
Точка P, також з цілими координатами, знаходиться на лінії AC так, щоб ABP, CDP і BDP були подібні.
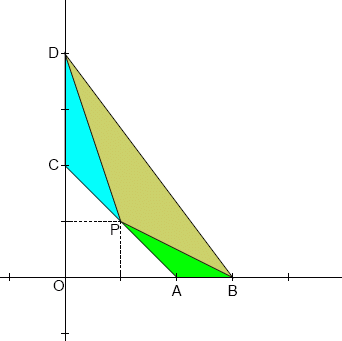
Легко довести, що трикутники можуть бути подібними, якщо a = c.
Отже, знаючи, що a = c, ми шукаємо триплети (a, b, d) де принаймні одна точка P (з цілими координатами) існує на AC, роблячи три подібні трикутники ABP, CDP та BDP.
Наприклад, якщо (a, b, d) = (2, 3, 4), можна легко підтвердити, що точка P(1, 1) задовольняє вимоги завдання. Зверніть увагу, що (2,3,4) і (2,4,3) вважаються окремими, хоча точка P(1, 1) для них спільна.
Якщо b + d < 100, то існує 92 триплети (a, b, d) у яких є точка P.
Якщо b + d < 100\\,000, то існує 320471 триплети (a, b, d), які мають точку P.
Якщо b + d < 100\\,000\\,000,скільки буде триплетів (a, b, d) з точкою P?
--hints--
threeSimilarTriangles() має повернути 549936643.
assert.strictEqual(threeSimilarTriangles(), 549936643);
--seed--
--seed-contents--
function threeSimilarTriangles() {
return true;
}
threeSimilarTriangles();
--solutions--
// solution required