78 lines
5.9 KiB
Markdown
78 lines
5.9 KiB
Markdown
---
|
||
title: Logistic Regression
|
||
---
|
||
## Logistic Regression
|
||
<br>
|
||
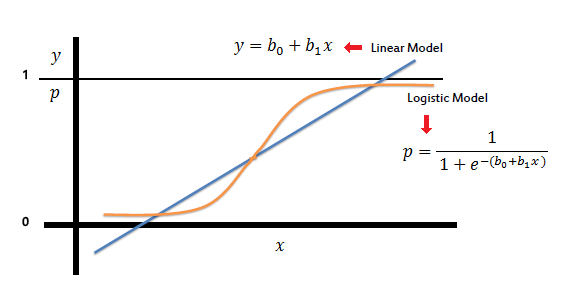
Logistic regression is very similar to linear regression As in both algorithms ,models are trained to find a regression line to define function for futher prediction.Therefore, It's a form of supervised learning, which tries to predict the responses of unlabeled, unseen data by first training with labeled data,on a set of observations which consists of both independent (X) and dependent (Y) variables. But while <a href='https://guide.freecodecamp.org/machine-learning/linear-regression' target='_blank'>Linear Regression</a> assumes that the response variable (Y) is quantitative or continuous, Logistic Regression is used specifically when the response variable is qualititative,or discrete.<br>
|
||
|
||
|
||
#### How it Works
|
||
Logistic regression models the probability that Y, the response variable, belongs to a certain category. In many cases, the response variable will be a binary one, so logistic regression will want to model a function y = f(x) that outputs a normalized value that ranges from, say, 0 to 1 for all values of X, corresponding to the two possible values of Y. It does this by using the logistic function:
|
||
Logistic regression is the appropriate regression analysis to conduct when the dependent variable is dichotomous (binary) But it has another form such as : mutivalued logistic regression which is used to classify for more than two classes. Like all regression analyses, the logistic regression is a predictive analysis. Logistic regression is used to describe data and to explain the relationship between one dependent binary variable and one or more nominal, ordinal, interval or ratio-level independent variables.
|
||
|
||
|
||
<br>
|
||
Logistic regression is used to solve classification problems, where the output is of the form y∈{0,1}. Here, 0 is a negative class and 1 is a positive class. Let's say we have a hypothesis hθ(x), where x is our dataset(a matrix) of length m. θ is the parameteric matrix. We have : 0 < hθ(x) < 1
|
||
|
||
In Logistic regression, hθ(x) is a sigmoid function, thus hθ(x) = g(θ'x).
|
||
A Sigmoid function is an appropriate function developed by statician to classify which always result between 0 or 1 depending on its
|
||
input attributes and weights(which is theta **θ** here)
|
||
g(θ'x) = 1/ 1 + e^(-θ'x)
|
||
|
||
Note: θ' is θ transpose.
|
||
**Transpose is used to multiply here it with attribute array It will be easily understoodable once you get in a bit depth with Linear algebra.**
|
||
|
||
#### Cost function
|
||
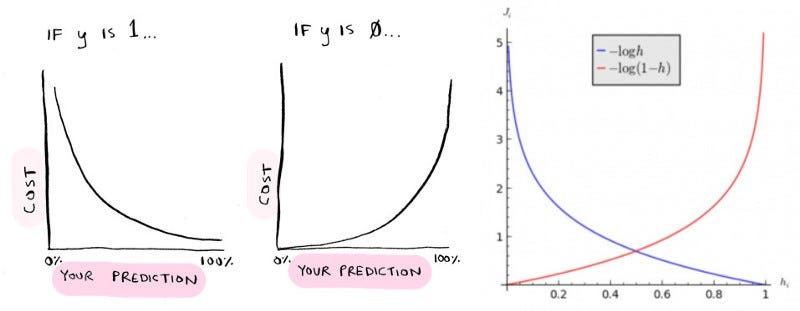
Cost Function is a measure of How much our, Hypothetic function is farther to the observed one .
|
||
The cost function used for Logistic regression is :
|
||
|
||
J(θ)=(1/m)∑Cost(hθ(x(i)),y(i)) , where summation is from i=1 to m.
|
||
|
||
Where hθ(x) is = hypothetic value calculated in accordance with attributes and wieghts which are calculated and balanced via algorithm such as gradient decent .
|
||
y = is the corresponding value from observation data set
|
||
|
||
Here cost function is not a proper sigmoid function in use but in place ,two log functions which performs with greater efficieny without
|
||
penalizing the learning algorithms are used.
|
||
Cost(hθ(x),y)=−log(hθ(x)) if y = 1
|
||
Cost(hθ(x),y)=−log(1−hθ(x)) if y = 0
|
||
|
||
#### Predictions using logistic regression:
|
||
Logistic regression models the probability of the default class(i.e. the first class).
|
||
You can classify results given by :
|
||
|
||
y = e^(b0 + b1*X) / (1 + e^(b0 + b1*X))
|
||
|
||
into two classes.Like for sigmoid function 0.5 is set as the decision boundary all x for which y≥0.5 are classified as class A and for which y<0.5 are classified as class B.
|
||
|
||
#### Multi class logistic regression:
|
||
Although you will see logistic regression usually being used in case of binary classification but you can also use it in case of classification into multiple classes by:
|
||
|
||
##### one vs one method:
|
||
Here a classifier for each class is created separately and the classifier with the highest score is considered as output.
|
||
|
||
##### one vs all method:
|
||
Here multiple(N*N(N-1)/2 where N=no. of classes) binary classifiers are made and then by comparing their scores the output is obtained.
|
||
|
||
#### Applications of logistic regression:
|
||
1) To classify mail as spam or not spam.<br>
|
||
2) To determine presence or absence of certain disease like cancer based on symptoms and other medical data
|
||
Like- benign or malignant.<br>
|
||
3) Classify images based on pixel data.
|
||
|
||
#### Logistic Regression Assumptions
|
||
Binary logistic regression requires the dependent variable to be binary.
|
||
For a binary regression, the factor level 1 of the dependent variable should represent the desired outcome.
|
||
Only the meaningful variables should be included.
|
||
The independent variables should be independent of each other. That is, the model should have little or no multicollinearity.
|
||
The independent variables are linearly related to the log odds.
|
||
Logistic regression requires quite large sample sizes.
|
||
|
||
|
||
#### More Information:
|
||
<!-- Please add any articles you think might be helpful to read before writing the article -->
|
||
For further reading to build logistic regression step by step :
|
||
|
||
- Click <a href="https://medium.com/towards-data-science/building-a-logistic-regression-in-python-step-by-step-becd4d56c9c8" target='_blank' rel='nofollow'>here</a> for an article about building a Logistic Regression in Python.
|
||
- Click <a href="http://nbviewer.jupyter.org/gist/justmarkham/6d5c061ca5aee67c4316471f8c2ae976" target='_blank' rel='nofollow'>here</a> for another article on building a Logical Regression.
|
||
- Click <a href="http://nbviewer.jupyter.org/gist/justmarkham/6d5c061ca5aee67c4316471f8c2ae976" target='_blank' rel='nofollow'>here</a> for another article on mathematics and intuition behind Logical Regression.
|