freeCodeCamp/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-163-cross-hatched-triangles.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f40f1000cf542c50ff22	Problem 163: Cross-hatched triangles	5	301797	problem-163-cross-hatched-triangles

--description--

Consider an equilateral triangle in which straight lines are drawn from each vertex to the middle of the opposite side, such as in the size 1 triangle in the sketch below.

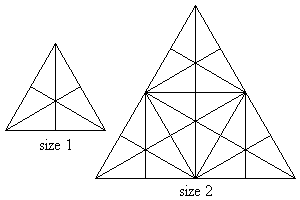
Sixteen triangles of either different shape or size or orientation or location can now be observed in that triangle. Using size 1 triangles as building blocks, larger triangles can be formed, such as the size 2 triangle in the above sketch. One-hundred and four triangles of either different shape or size or orientation or location can now be observed in that size 2 triangle.

It can be observed that the size 2 triangle contains 4 size 1 triangle building blocks. A size 3 triangle would contain 9 size 1 triangle building blocks and a size n triangle would thus contain n^2 size 1 triangle building blocks.

If we denote T(n) as the number of triangles present in a triangle of size n, then

$$\begin{align} & T(1) = 16 \\ & T(2) = 104 \end{align}$$

Find T(36).

--hints--

crossHatchedTriangles() should return 343047.

assert.strictEqual(crossHatchedTriangles(), 343047);

--seed--

--seed-contents--

function crossHatchedTriangles() {

  return true;
}

crossHatchedTriangles();

--solutions--

// solution required