5a52c229f5
* fix: clean-up Project Euler 181-200 * fix: corrections from review Co-authored-by: Tom <20648924+moT01@users.noreply.github.com> * fix: missing delimiter Co-authored-by: Tom <20648924+moT01@users.noreply.github.com>
1.8 KiB
1.8 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f42f1000cf542c50ff40 | Problem 194: Coloured Configurations | 5 | 301832 | problem-194-coloured-configurations |
--description--
Consider graphs built with the units A:
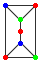and B: 
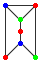, where the units are glued along the vertical edges as in the graph 
.
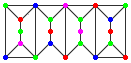A configuration of type (a,b,c) is a graph thus built of a units A and b units B, where the graph's vertices are coloured using up to c colours, so that no two adjacent vertices have the same colour. The compound graph above is an example of a configuration of type (2,2,6), in fact of type (2,2,c) for all c ≥ 4
Let N(a,b,c) be the number of configurations of type (a,b,c). For example, N(1,0,3) = 24, N(0,2,4) = 92928 and N(2,2,3) = 20736.
Find the last 8 digits of N(25,75,1984).
--hints--
coloredConfigurations() should return 61190912.
assert.strictEqual(coloredConfigurations(), 61190912);
--seed--
--seed-contents--
function coloredConfigurations() {
return true;
}
coloredConfigurations();
--solutions--
// solution required