freeCodeCamp/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-289-eulerian-cycles.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f48d1000cf542c50ffa0	Problem 289: Eulerian Cycles	5	301940	problem-289-eulerian-cycles

--description--

Let C(x,y) be a circle passing through the points (x, y), (x, y + 1), (x + 1, y) and (x + 1, y + 1).

For positive integers m and n, let E(m,n) be a configuration which consists of the m·n circles: { C(x,y): 0 ≤ x < m, 0 ≤ y < n, x and y are integers }

An Eulerian cycle on E(m,n) is a closed path that passes through each arc exactly once. Many such paths are possible on E(m,n), but we are only interested in those which are not self-crossing: A non-crossing path just touches itself at lattice points, but it never crosses itself.

The image below shows E(3,3) and an example of an Eulerian non-crossing path.

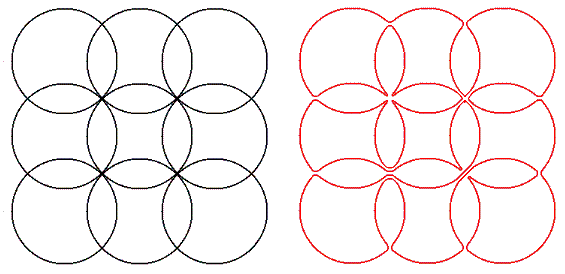
Let L(m,n) be the number of Eulerian non-crossing paths on E(m,n). For example, L(1,2) = 2, L(2,2) = 37 and L(3,3) = 104290.

Find L(6,10)\bmod {10}^{10}.

--hints--

eulerianCycles() should return 6567944538.

assert.strictEqual(eulerianCycles(), 6567944538);

--seed--

--seed-contents--

function eulerianCycles() {

  return true;
}

eulerianCycles();

--solutions--

// solution required