freeCodeCamp/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-385-ellipses-inside-triangles.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f4ee1000cf542c510000	Problem 385: Ellipses inside triangles	5	302049	problem-385-ellipses-inside-triangles

--description--

For any triangle T in the plane, it can be shown that there is a unique ellipse with largest area that is completely inside T.

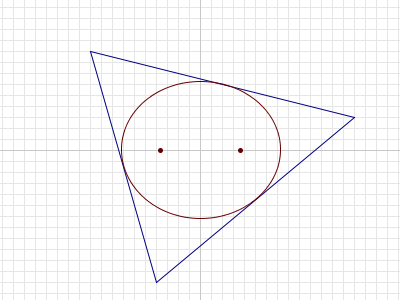
For a given n, consider triangles T such that:

• the vertices of T have integer coordinates with absolute value ≤ n, and
• the foci¹ of the largest-area ellipse inside T are (\sqrt{13}, 0) and (-\sqrt{13}, 0).

Let A(n) be the sum of the areas of all such triangles.

For example, if n = 8, there are two such triangles. Their vertices are (-4,-3), (-4,3), (8,0) and (4,3), (4,-3), (-8,0), and the area of each triangle is 36. Thus A(8) = 36 + 36 = 72.

It can be verified that A(10) = 252, A(100) = 34\\,632 and A(1000) = 3\\,529\\,008.

Find A(1\\,000\\,000\\,000).

¹The foci (plural of focus) of an ellipse are two points A and B such that for every point P on the boundary of the ellipse, AP + PB is constant.

--hints--

ellipsesInsideTriangles() should return 3776957309612154000.

assert.strictEqual(ellipsesInsideTriangles(), 3776957309612154000);

--seed--

--seed-contents--

function ellipsesInsideTriangles() {

  return true;
}

ellipsesInsideTriangles();

--solutions--

// solution required