freeCodeCamp/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-428-necklace-of-circles.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f5191000cf542c51002b	Problem 428: Necklace of Circles	5	302098	problem-428-necklace-of-circles

--description--

Let a, b and c be positive numbers.

Let W, X, Y, Z be four collinear points where |WX| = a, |XY| = b, |YZ| = c and |WZ| = a + b + c.

Let C_{\text{in}} be the circle having the diameter XY.

Let C_{\text{out}} be the circle having the diameter WZ.

The triplet (a, b, c) is called a necklace triplet if you can place k ≥ 3 distinct circles C_1, C_2, \ldots, C_k such that:

• C_i has no common interior points with any C_j for 1 ≤ i, j ≤ k and i ≠ j,
• C_i is tangent to both C_{\text{in}} and C_{\text{out}} for 1 ≤ i ≤ k,
• C_i is tangent to C_{i + 1} for 1 ≤ i < k, and
• C_k is tangent to C_1.

For example, (5, 5, 5) and (4, 3, 21) are necklace triplets, while it can be shown that (2, 2, 5) is not.

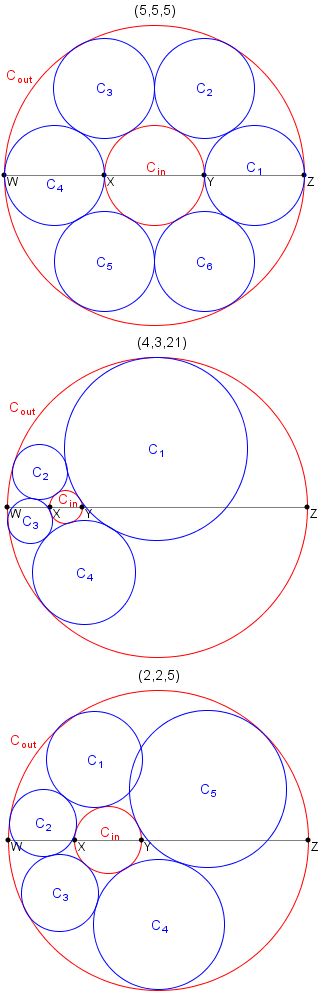
Let T(n) be the number of necklace triplets (a, b, c) such that a, b and c are positive integers, and b ≤ n. For example, T(1) = 9, T(20) = 732 and T(3\\,000) = 438\\,106.

Find T(1\\,000\\,000\\,000).

--hints--

necklace(1000000000) should return 747215561862.

assert.strictEqual(necklace(1000000000), 747215561862);

--seed--

--seed-contents--

function necklace(n) {

  return true;
}

necklace(1000000000)

--solutions--

// solution required