freeCodeCamp/guide/english/algorithms/greatest-common-divisor-euclidean/index.md

---
title: Greatest Common Divisor Euclidean
---
## Greatest Common Divisor Euclidean

For this topic you must know about Greatest Common Divisor (GCD) and the MOD operation first.

#### Greatest Common Divisor (GCD)
The GCD of two or more integers is the largest integer that divides each of the integers such that their remainder is zero.

Example-  
GCD of 20, 30 = 10 *(10 is the largest number which divides 20 and 30 with remainder as 0)*  
GCD of 42, 120, 285 = 3 *(3 is the largest number which divides 42, 120 and 285 with remainder as 0)*  

#### "mod" Operation
The mod operation gives you the remainder when two positive integers are divided.
We write it as follows-  
`A mod B = R`

This means, dividing A by B gives you the remainder R, this is different than your division operation which gives you the quotient.

Example-  
7 mod 2 = 1 *(Dividing 7 by 2 gives the remainder 1)*  
42 mod 7 = 0 *(Dividing 42 by 7 gives the remainder 0)*  

With the above two concepts understood you will easily understand the Euclidean Algorithm.

### Euclidean Algorithm for Greatest Common Divisor (GCD)
The Euclidean Algorithm finds the GCD of 2 numbers.

You will better understand this Algorithm by seeing it in action.
Assuming you want to calculate the GCD of  1220 and 516, lets apply the Euclidean Algorithm-  

Assuming you want to calculate the GCD of  1220 and 516, lets apply the Euclidean Algorithm-
![Euclidean Example](https://cdn-media-1.freecodecamp.org/imgr/aa8oGgP.png)  

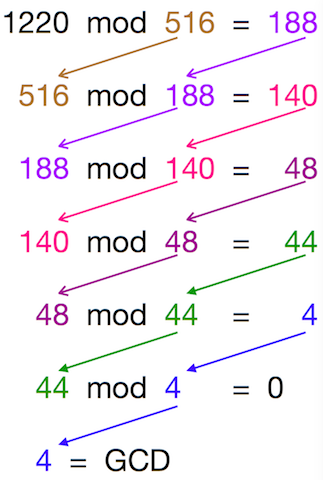
Pseudo Code of the Algorithm-  
Step 1: **Let `a, b` be the two numbers**  
Step 2: **`a mod b = R`**  
Step 3: **Let `a = b` and `b = R`**  
Step 4: **Repeat Steps 2 and 3 until `a mod b` is greater than 0**  
Step 5: **GCD = b**  
Step 6: Finish  

JavaScript Code to Perform GCD-
```javascript
function gcd(a, b) {
  var R;
  while ((a % b) > 0)  {
    R = a % b;
    a = b;
    b = R;
  }
  return b;
}
```

JavaScript Code to Perform GCD using Recursion-
```javascript
function gcd(a, b) {
  if (b == 0)
    return a;
  else
    return gcd(b, (a % b));
}
```

C code to perform GCD using recursion
```c
int gcd(int a, int b) 
{ 
    // Everything divides 0  
    if (a == 0) 
       return b; 
    if (b == 0) 
       return a; 
  
    // base case 
    if (a == b) 
        return a; 
  
    // a is greater 
    if (a > b) 
        return gcd(a-b, b); 
    return gcd(a, b-a); 
}
```

C++ Code to Perform GCD-
```csharp
int gcd(int a,int b) {
  int R;
  while ((a % b) > 0)  {
    R = a % b;
    a = b;
    b = R;
  }
  return b;
}
```

Python Code to Perform GCD using Recursion
```Python
def gcd(a, b):
  if b == 0:
    return a:
  else:
    return gcd(b, (a % b))
```

Java Code to Perform GCD using Recursion
```Java
static int gcd(int a, int b)
{
  if(b == 0)
  {
    return a;
  }
  return gcd(b, a % b);
}

```

You can also use the Euclidean Algorithm to find GCD of more than two numbers.
Since, GCD is associative, the following operation is valid- `GCD(a,b,c) == GCD(GCD(a,b), c)`

Calculate the GCD of the first two numbers, then find GCD of the result and the next number.
Example- `GCD(203,91,77) == GCD(GCD(203,91),77) == GCD(7, 77) == 7`

You can find GCD of `n` numbers in the same way.

### Extended Euclidean algorithm
This is an extension of Euclidean algorithm. It also calculates the coefficients x, y such that 

ax+by = gcd(a,b)

x and y are also known as coefficients of Bézout's identity.

c code for Extended Euclidean algorithm

```c
struct Triplet{
	int gcd;
	int x;
	int y;
};
Triplet gcdExtendedEuclid(int a,int b){
	//Base Case
	if(b==0){
		Triplet myAns;
		myAns.gcd = a;
		myAns.x = 1;
		myAns.y = 0;
		return myAns;

	}
	Triplet smallAns = gcdExtendedEuclid(b,a%b);
	//Extended euclid says

	Triplet myAns;
	myAns.gcd = smallAns.gcd;
	myAns.x  = smallAns.y;
	myAns.y = (smallAns.x - ((a/b)*(smallAns.y)));
	return myAns;	
}
```