freeCodeCamp/guide/english/logic/algebra-of-logic/index.md

title

title
Algebra of Logic

Algebra of Logic

Algebra of Logic or Boolean algebra is a branch of mathematics. It deals with variables and their truth value. The variables have two possible states – true or false.

It was first introduced by George Boole in his book The Mathematical Analysis of Logic (1847), and was subsequently developed by C.S. Peirce, P.S. Poretskii, B. Russell, D. Hilbert, and others. The development of the algebra of logic was an attempt to solve traditional logical problems by algebraic methods.

Boolean algebra is fundamental to the development of digital electronics. It is responsible for making possible all modern computing.

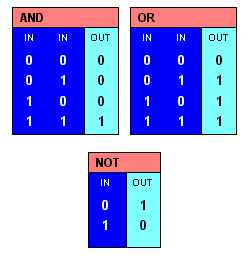
The three basic operations in Boolean Algebra are AND, OR, and NOT. Most often
AND is also represented by .(dot)
OR is also represented by +(plus)
NOT is also represented by ~(tilde)
Consider two boolean variables x and y:

• x AND y is true if and only if both x and y are true
• x OR y is true if either of x or y are true
• NOT x is true if and only if x is false and vice versa

NOT of boolean statements can be refactored to apply directly to each variable. Consider the following :

• NOT (x AND y) = NOT x OR NOT y
• NOT (x OR y) = NOT x AND NOT y

The above statements are called "De Morgan's Laws." This is a very useful and important law in Boolean Algebra.

More Information:

• Boolean algebra article: Wikipedia
• The Calculus of Logic: George Boole
• Boolean Algebra Demonstration: Wolfram MathWorld
• De Morgan's laws: Wikipedia