52 lines
6.1 KiB
Markdown
52 lines
6.1 KiB
Markdown
---
|
||
title: AVL Trees
|
||
localeTitle: Деревья AVL
|
||
---
|
||
## Деревья AVL
|
||
|
||
Дерево AVL является подтипом двоичного дерева поиска.
|
||
|
||
BST представляет собой структуру данных, состоящую из узлов. Он имеет следующие гарантии:
|
||
|
||
1. Каждое дерево имеет корневой узел (вверху).
|
||
2. Корневой узел имеет ноль или более дочерних узлов.
|
||
3. Каждый дочерний узел имеет ноль или более дочерних узлов и т. Д.
|
||
4. Каждый узел имеет до двух детей.
|
||
5. Для каждого узла его левые потомки меньше текущего узла, что меньше, чем у правых потомков.
|
||
|
||
У деревьев AVL есть дополнительная гарантия:
|
||
|
||
6. Разница между глубиной правого и левого поддеревьев не может быть больше одной. Чтобы сохранить эту гарантию, реализация AVL будет включать в себя алгоритм для балансировки дерева при добавлении дополнительного элемента, который нарушит эту гарантию.
|
||
|
||
Деревья AVL имеют наихудший поиск, вставку и удаление времени O (log n).
|
||
|
||
### Правильное вращение
|
||
|
||
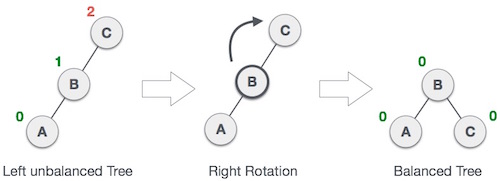
|
||
|
||
### Левое вращение
|
||
|
||
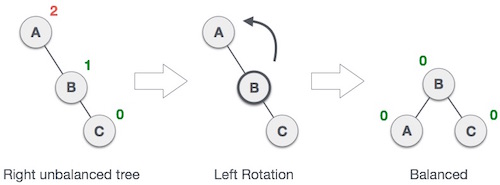
|
||
|
||
### Процесс вставки AVL
|
||
|
||
Вы сделаете вставку, похожую на обычную вставку двоичного поиска. После вставки вы исправляете свойство AVL с помощью поворота влево или вправо.
|
||
|
||
* Если есть дисбаланс в левом дочернем элементе правого поддерева, то вы выполняете поворот влево-вправо.
|
||
* Если есть дисбаланс в левом дочернем элементе левого поддерева, то вы выполняете правильное вращение.
|
||
* Если есть дисбаланс в правильном дочернем элементе правого поддерева, то вы выполняете левое вращение.
|
||
* Если есть дисбаланс в правом дочернем элементе левого поддерева, то вы выполняете правое-левое вращение.
|
||
|
||
#### Дополнительная информация:
|
||
|
||
[YouTube - AVL Tree](https://www.youtube.com/watch?v=7m94k2Qhg68)
|
||
|
||
Дерево AVL является самобалансирующимся двоичным деревом поиска. Дерево AVL представляет собой двоичное дерево поиска, которое имеет следующие свойства: -> Под деревья каждого узла отличаются высотой не более одного. -> Каждое поддерево является деревом AVL.
|
||
|
||
Дерево AVL проверяет высоту левого и правого поддеревьев и гарантирует, что разница не больше 1. Это различие называется коэффициентом баланса. Высота дерева AVL всегда равна O (Logn), где n - количество узлов в дереве.
|
||
|
||
Вращение дерева AVL: -
|
||
|
||
В дереве AVL после выполнения каждой операции, такой как вставка и удаление, нам нужно проверить коэффициент баланса каждого узла в дереве. Если каждый узел удовлетворяет условию баланса, то мы завершаем операцию, иначе мы должны сбалансировать ее. Мы используем операции поворота, чтобы дерево сбалансировалось всякий раз, когда дерево становится несбалансированным из-за какой-либо операции.
|
||
|
||
Операции вращения используются, чтобы сбалансировать дерево. Существует четыре оборота, и они подразделяются на два типа: -> Одиночное левое вращение (вращение LL) В LL Rotation каждый узел перемещает одну позицию влево от текущей позиции. -> Одиночное правое вращение (вращение RR) В RR Rotation каждый узел перемещает одну позицию вправо от текущей позиции. -> Вращение влево вправо (вращение LR) LR Rotation - комбинация одиночного левого вращения, за которым следует однократное вращение. В LR Rotation сначала каждый узел перемещает одну позицию влево, затем одну позицию вправо от текущей позиции. -> Вращение вправо влево (вращение RL) RL Rotation - комбинация одиночного правого вращения, за которым следует однократное вращение влево. В RL Rotation сначала каждый узел перемещает одну позицию вправо, затем одну позицию слева от текущей позиции. |