freeCodeCamp/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-265-binary-circles.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f4761000cf542c50ff88	Problem 265: Binary Circles	5	301914	problem-265-binary-circles

--description--

2^N binary digits can be placed in a circle so that all the $N$-digit clockwise subsequences are distinct.

For N = 3, two such circular arrangements are possible, ignoring rotations:

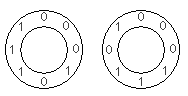
For the first arrangement, the 3-digit subsequences, in clockwise order, are: 000, 001, 010, 101, 011, 111, 110 and 100.

Each circular arrangement can be encoded as a number by concatenating the binary digits starting with the subsequence of all zeros as the most significant bits and proceeding clockwise. The two arrangements for N = 3 are thus represented as 23 and 29:

$${00010111}_2 = 23\\ {00011101}_2 = 29$$

Calling S(N) the sum of the unique numeric representations, we can see that S(3) = 23 + 29 = 52.

Find S(5).

--hints--

binaryCircles() should return 209110240768.

assert.strictEqual(binaryCircles(), 209110240768);

--seed--

--seed-contents--

function binaryCircles() {

  return true;
}

binaryCircles();

--solutions--

// solution required