freeCodeCamp/guide/arabic/algorithms/binary-search-trees/index.md

---
title: Binary Search Trees
localeTitle: أشجار البحث الثنائي
---
## أشجار البحث الثنائي

![شجرة البحث الثنائية](https://cdn-images-1.medium.com/max/1320/0*x5o1G1UpM1RfLpyx.png)

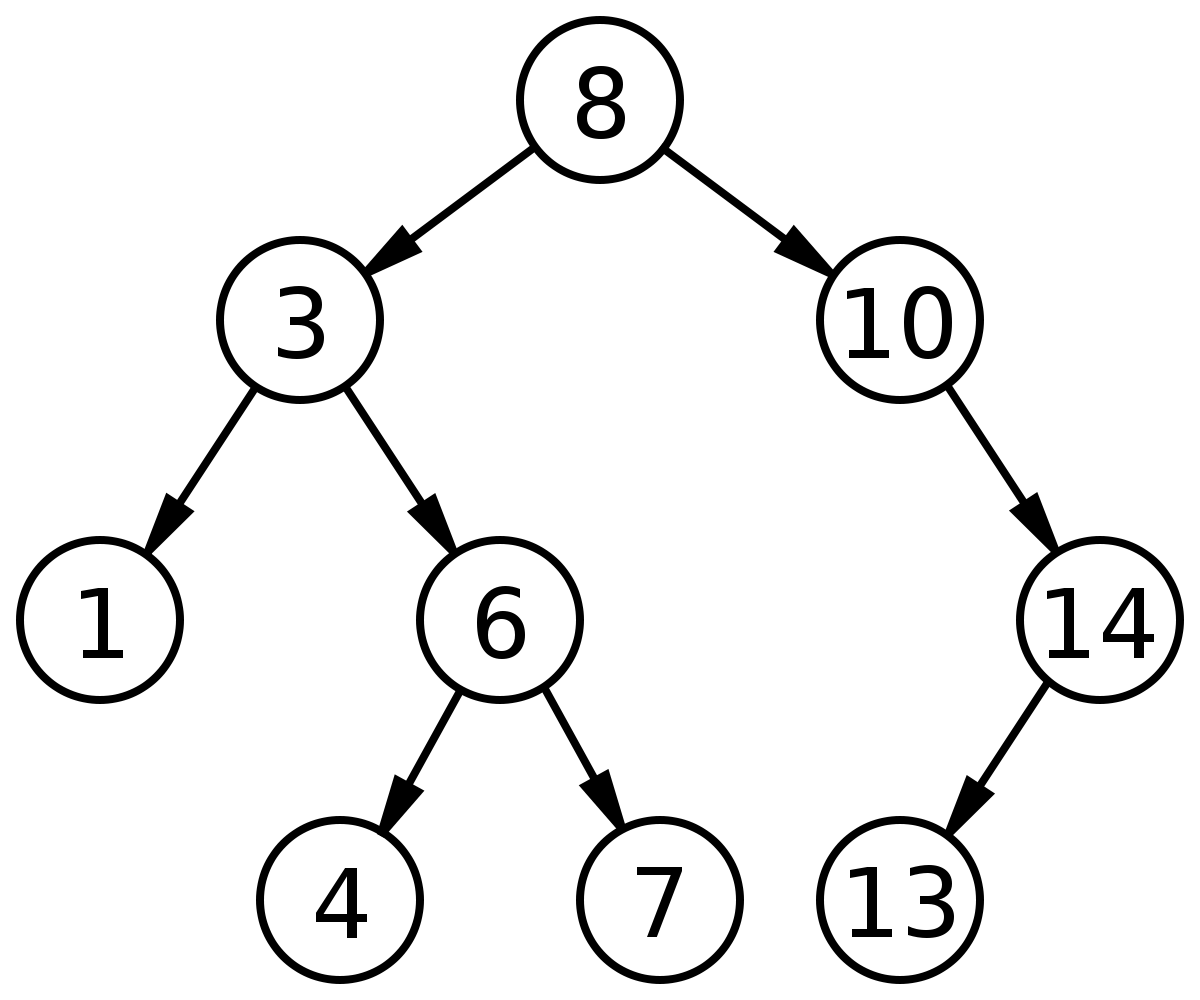
الشجرة هي بنية بيانات تتكون من عقد لها الخصائص التالية:

1.  كل شجرة لديها عقدة جذرية (في الجزء العلوي) لديها بعض القيمة.
2.  العقدة الجذرية لديها صفر أو أكثر من العقد التابعة.
3.  كل عقدة طفل لديها صفر أو أكثر العقد التابعة ، وهلم جرا. هذا إنشاء شجرة فرعية في الشجرة. تحتوي كل عقدة على شجرة فرعية خاصة بها تتكون من أطفاله وأطفالهم ، إلخ. وهذا يعني أن كل عقدة بمفردها يمكن أن تكون شجرة.

تضيف شجرة البحث الثنائية (BST) هاتين الخاصيتين:

1.  كل عقدة لديها حد أقصى يصل إلى طفلين.
2.  لكل عقدة ، تكون قيم العقد المتسلسلة اليسرى أقل من عقدة العقدة الحالية ، والتي بدورها تكون أقل من العقد التناسلية الصحيحة (إن وجدت).

يتم إنشاء BST على فكرة خوارزمية [البحث الثنائي](https://guide.freecodecamp.org/algorithms/search-algorithms/binary-search) ، والتي تسمح [بالبحث](https://guide.freecodecamp.org/algorithms/search-algorithms/binary-search) السريع وإدخال وإزالة العقد. إن الطريقة التي يتم بها إعدادها تعني أنه في المتوسط ​​، تسمح كل مقارنة للعمليات بتخطي حوالي نصف الشجرة ، بحيث يستغرق كل بحث أو إدراج أو حذف وقتًا متناسبًا مع لوغاريتم عدد العناصر المخزنة في الشجرة ، `O(log n)` . ومع ذلك ، في بعض الأحيان يمكن أن يحدث أسوأ الحالات ، عندما تكون الشجرة غير متوازنة ويكون تعقيد الوقت هو `O(n)` لكل هذه الوظائف الثلاثة. هذا هو السبب في أشجار التوازن الذاتي (AVL ، أحمر أسود ، وما إلى ذلك) هي أكثر فعالية من BST الأساسية.

**أسوأ مثال على سيناريو الحالة:** يمكن أن يحدث هذا عند الاستمرار في إضافة العقد التي تكون _دائمًا_ أكبر من العقدة قبل (إنه الأصل) ، ويمكن أن يحدث نفس الشيء عندما تقوم دائمًا بإضافة العقد ذات القيم الأقل من أولياء أمورهم.

### العمليات الأساسية على BST

*   إنشاء: ينشئ شجرة فارغة.
*   إدراج: إدراج عقدة في الشجرة.
*   بحث: يبحث عن عقدة في الشجرة.
*   حذف: لحذف عقدة من الشجرة.

#### خلق

في البداية يتم إنشاء شجرة فارغة بدون أي عقد. تتم تهيئة المتغير / المعرف الذي يجب أن يشير إلى عقدة الجذر بقيمة `NULL` .

#### بحث

تبدأ دائمًا في البحث عن الشجرة في عقدة الجذر والنزول من هناك. يمكنك مقارنة البيانات في كل عقدة مع تلك التي تبحث عنها. إذا لم تتطابق العقدة المقارنة ، فإما أن تنتقل إلى الطفل الصحيح أو الطفل الأيسر ، والذي يعتمد على نتيجة المقارنة التالية: إذا كانت العقدة التي تبحث عنها أقل من تلك التي كنت تقارنها بها ، تنتقل إلى الطفل الأيسر ، وإلا (إذا كان أكبر) ، فانتقل إلى الطفل الصحيح. لماذا ا؟ نظرًا لأن BST منظم (وفقًا لتعريفه) ، فإن الطفل المناسب دائمًا يكون أكبر من الأصل وأن الطفل الأيسر يكون دائمًا أقل.

#### إدراج

انها تشبه الى حد بعيد وظيفة البحث. تبدأ مرة أخرى عند جذر الشجرة وتنزل بشكل متكرر ، حيث تبحث عن المكان المناسب لإدخال العقدة الجديدة ، بنفس الطريقة الموضحة في وظيفة البحث. إذا كانت العقدة ذات القيمة نفسها موجودة بالفعل في الشجرة ، يمكنك اختيار إما إدراج التكرار أم لا. بعض الأشجار تسمح بوجود نسخ مكررة ، والبعض الآخر لا يسمح بذلك. ذلك يعتمد على تنفيذ معين.

#### حذف

هناك 3 حالات يمكن أن تحدث عندما تحاول حذف عقدة. إذا كان لديه،

1.  لا توجد شجرة فرعية (لا يوجد أطفال): هذا هو الأسهل. يمكنك ببساطة حذف العقدة ، دون أي إجراءات إضافية مطلوبة.
2.  شجرة فرعية واحدة (طفل واحد): يجب عليك التأكد من أنه بعد حذف العقدة ، يتم توصيل الطفل التابع له إلى أصل العقدة المحذوفة.
3.  صفحتان فرعيتان (طفلين): عليك البحث عن واستبدال العقدة التي تريد حذفها مع خلفها (العقدة الفاتنة في الشجرة الفرعية الصحيحة).

وقت تعقيد إنشاء الشجرة هو `O(1)` . يعتمد تعقيد وقت البحث عن عقدة أو إدخالها أو حذفها على ارتفاع الشجرة `h` ، لذا فإن الحالة الأسوأ هي `O(h)` .

#### سلف عقدة

يمكن وصف الإصدارات السابقة بأنها العقدة التي ستظهر قبل العقدة التي أنت فيها حاليًا. للعثور على سابق العقدة الحالية ، ابحث عن العقدة اليمنى الأكبر / الأكبر في الشجرة الفرعية اليسرى.

#### خلف العقدة

يمكن وصف الخلفاء على أنهم العقدة التي تأتي بعد العقدة التي أنت فيها حاليًا. للعثور على خليفة العقدة الحالية ، انظر إلى العقدة اليسرى / أقصى اليسار في الشجرة الفرعية اليمنى.

### أنواع خاصة من BT

*   كومة
*   شجرة حمراء سوداء
*   B-شجرة
*   شجرة سبلاي
*   شجرة N-ary
*   تري (شجرة الجذر)

### وقت التشغيل

**هيكل البيانات: صفيف**

*   أسوأ حالة أداء: `O(log n)`
*   أداء أفضل أداء: `O(1)`
*   متوسط ​​الأداء: `O(log n)`
*   أسوأ تعقيد في الفضاء: `O(1)`

حيث `n` هو عدد العقد في BST.

### تنفيذ BST

وإليك تعريفًا لعقدة BST التي تحتوي على بعض البيانات ، مع الإشارة إلى عقد الطفل اليمنى واليسرى.

```c
struct node {
   int data;
   struct node *leftChild;
   struct node *rightChild;
};
``` 

#### عملية البحث

عندما يتم البحث عن عنصر ، ابدأ البحث من العقدة الجذرية. ثم إذا كانت البيانات أقل من قيمة المفتاح ، فابحث عن العنصر في الشجرة الفرعية اليسرى. خلاف ذلك ، ابحث عن العنصر في الشجرة الفرعية الصحيحة. اتبع نفس الخوارزمية لكل عقدة.

 `struct node* search(int data){ 
   struct node *current = root; 
   printf("Visiting elements: "); 
 
   while(current->data != data){ 
 
      if(current != NULL) { 
         printf("%d ",current->data); 
 
         //go to left tree 
         if(current->data > data){ 
            current = current->leftChild; 
         }//else go to right tree 
         else { 
            current = current->rightChild; 
         } 
 
         //not found 
         if(current == NULL){ 
            return NULL; 
         } 
      } 
   } 
   return current; 
 } 
` 

#### أدخل العملية

عندما يتم إدراج عنصر ، حدد موقعه الصحيح أولاً. ابدأ البحث من العقدة الجذرية ، ثم إذا كانت البيانات أقل من قيمة المفتاح ، ابحث عن الموقع الفارغ في الشجرة الفرعية اليسرى وأدخل البيانات. وإلا ، فابحث عن الموقع الفارغ في الشجرة الفرعية الصحيحة وأدخل البيانات.

 `void insert(int data) { 
   struct node *tempNode = (struct node*) malloc(sizeof(struct node)); 
   struct node *current; 
   struct node *parent; 
 
   tempNode->data = data; 
   tempNode->leftChild = NULL; 
   tempNode->rightChild = NULL; 
 
   //if tree is empty 
   if(root == NULL) { 
      root = tempNode; 
   } else { 
      current = root; 
      parent = NULL; 
 
      while(1) { 
         parent = current; 
 
         //go to left of the tree 
         if(data < parent->data) { 
            current = current->leftChild; 
            //insert to the left 
 
            if(current == NULL) { 
               parent->leftChild = tempNode; 
               return; 
            } 
         }//go to right of the tree 
         else { 
            current = current->rightChild; 
 
            //insert to the right 
            if(current == NULL) { 
               parent->rightChild = tempNode; 
               return; 
            } 
         } 
      } 
   } 
 } 
` 

تتيح لنا أيضًا أشجار البحث الثنائي (BSTs) الوصول السريع إلى الأسلاف والخلفاء. يمكن وصف الإصدارات السابقة بأنها العقدة التي ستظهر قبل العقدة التي أنت فيها حاليًا.

*   للعثور على سابق العقدة الحالية ، انظر إلى العقدة الموجودة في أقصى اليمين / أعلى ورقة في الشجرة الفرعية اليسرى. يمكن وصف الخلفاء على أنهم العقدة التي تأتي بعد العقدة التي أنت فيها حاليًا.
*   للعثور على خليفة العقدة الحالية ، انظر إلى العقدة في أقصى اليسار / أصغر ورقة في الشجرة الفرعية اليمنى.

### دعونا ننظر في اثنين من الإجراءات التي تعمل على الأشجار.

بما أن الأشجار يتم تعريفها بشكل متكرر ، فمن الشائع جدًا كتابة الإجراءات الروتينية التي تعمل على أشجار متكررة.

على سبيل المثال ، إذا أردنا حساب ارتفاع الشجرة ، وهذا هو ارتفاع العقدة الجذرية ، يمكننا المضي قدمًا وبشكل متكرر ، من خلال الانتقال إلى الشجرة. لذلك يمكننا القول:

*   على سبيل المثال ، إذا كان لدينا شجرة صفراء ، فإن ارتفاعها يبلغ 0.
*   بخلاف ذلك ، نحن 1 زائد الحد الأقصى لشجرة الطفل اليسرى والشجرة الفرعية المناسبة.
*   لذلك إذا نظرنا إلى ورقة على سبيل المثال ، فإن هذا الارتفاع سيكون 1 لأن ارتفاع الطفل الأيسر هو صفر ، هو 0 ، وارتفاع الطفل الأيمن صفر هو أيضا 0. لذا فإن الحد الأقصى لذلك هو 0 ، ثم 1 زائد 0.

#### خوارزمية الارتفاع (شجرة)

```
if tree = nil:
    return 0
return 1 + Max(Height(tree.left),Height(tree.right))
``` 

#### هنا هو رمز في C ++

 `int maxDepth(struct node* node) 
 { 
    if (node==NULL) 
        return 0; 
   else 
   { 
       int rDepth = maxDepth(node->right); 
       int lDepth = maxDepth(node->left); 
 
       if (lDepth > rDepth) 
       { 
           return(lDepth+1); 
       } 
       else 
       { 
            return(rDepth+1); 
       } 
   } 
 } 
` 

يمكن أن ننظر أيضا في حساب حجم الشجرة التي هي عدد العقد.

*   مرة أخرى ، إذا كان لدينا شجرة لا شيء ، لدينا عقد الصفر.
*   خلاف ذلك ، لدينا عدد العقد في الطفل الأيسر بالإضافة إلى 1 لأنفسنا بالإضافة إلى عدد العقد في الطفل الصحيح. 1 بالإضافة إلى حجم الشجرة اليسرى بالإضافة إلى حجم الشجرة الصحيحة.

#### خوارزمية الحجم (شجرة)

```
if tree = nil
    return 0
return 1 + Size(tree.left) + Size(tree.right)
``` 

#### هنا هو رمز في C ++

```
int treeSize(struct node* node)
{
    if (node==NULL)
        return 0;
    else
        return 1+(treeSize(node->left) + treeSize(node->right));
}
``` 

### مقاطع الفيديو ذات الصلة على قناة YouTube freeCodeCamp

*   [شجرة البحث الثنائية](https://youtu.be/5cU1ILGy6dM)
*   [شجرة البحث الثنائية: عبور والطول](https://youtu.be/Aagf3RyK3Lw)

### فيما يلي الأنواع الشائعة من الأشجار الثنائية:

Full Binary Tree / Strict Binary Tree: شجرة ثنائية ممتلئة أو صارمة إذا كان لكل عقدة 0 أو 2 أطفال.

 `           18 
       /       \ 
     15         30 
    /  \        /  \ 
  40    50    100   40 
` 

في شجرة الثنائي الكاملة ، عدد العقد الورقية يساوي عدد العقد الداخلية زائد واحد.

إكمال Binary Tree: A Binary Tree اكتمال Binary Tree إذا تمت تعبئة كافة المستويات تمامًا باستثناء المستوى الأخير ، بينما يحتوي المستوى الأخير على كافة المفاتيح التي تم تركها قدر الإمكان

 `           18 
       /       \ 
     15         30 
    /  \        /  \ 
  40    50    100   40 
 /  \   / 
 8   7  9 
`