75 lines
3.1 KiB
Markdown
75 lines
3.1 KiB
Markdown
---
|
|
title: Greatest Common Divisor Euclidean
|
|
localeTitle: أعظم القاسم المشترك Euclidean
|
|
---
|
|
## أعظم القاسم المشترك Euclidean
|
|
|
|
لهذا الموضوع يجب أن تعرف عن القاسم المشترك الأكبر (GCD) وعملية MOD أولاً.
|
|
|
|
#### أعظم القاسم المشترك (GCD)
|
|
|
|
يعد GCD من عددين أو أكثر هو العدد الصحيح الأكبر الذي يقسم كل من الأعداد الصحيحة بحيث يكون الباقي صفرًا.
|
|
|
|
مثال-
|
|
GCD of 20، 30 = 10 _(10 is the أكبر رقم يقسم 20 و 30 والباقي على 0)_
|
|
GCD من 42 و 120 و 285 = 3 _(3 هو أكبر عدد يقسم 42 و 120 و 285 مع الباقي مثل 0)_
|
|
|
|
#### عملية "mod"
|
|
|
|
يعطيك عملية التعديل الباقي عندما يتم تقسيم عدد صحيح موجب. نكتبها على النحو التالي
|
|
`A mod B = R`
|
|
|
|
وهذا يعني أن قسمة A إلى B تعطيك الباقي R ، وهذا يختلف عن عملية القسمة التي تعطيك القسمة.
|
|
|
|
مثال-
|
|
7 mod 2 = 1 _(يُقسم القسمان 7 في 2 الباقي 1)_
|
|
42 mod 7 = 0 _(يعطي التقسيم 42 في 7 الباقي 0)_
|
|
|
|
مع المفهومين أعلاه المفهوم سوف تفهم بسهولة خوارزمية الإقليدية.
|
|
|
|
### خوارزمية الإقليدية لأعظم مقام مشترك (GCD)
|
|
|
|
وجدت الخوارزمية الإقليدية GCD من رقمين.
|
|
|
|
ستفهم هذه الخوارزمية بشكل أفضل من خلال رؤيتها أثناء العمل. على افتراض أنك تريد حساب GCD من 1220 و 516 ، يتيح تطبيق الخوارزمية الإقليدية ،
|
|
|
|
على افتراض أنك تريد حساب GCD من 1220 و 516 ، يتيح تطبيق الخوارزمية الإقليدية ، 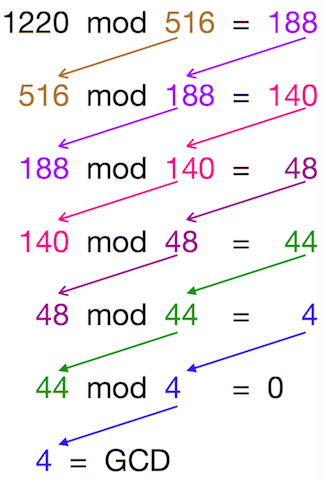
|
|
|
|
الكود الزائف للخوارزمية
|
|
الخطوة 1: **دع `a, b` يكون الرقمان**
|
|
الخطوة 2: **`a mod b = R`**
|
|
الخطوة 3: **دع `a = b` و `b = R`**
|
|
الخطوة 4: **كرر الخطوتين 2 و 3 حتى `a mod b` أكبر من 0**
|
|
الخطوة 5: **GCD = ب**
|
|
الخطوة 6: الانتهاء
|
|
|
|
شفرة جافا سكريبت لتنفيذ GCD-
|
|
|
|
```javascript
|
|
function gcd(a, b) {
|
|
var R;
|
|
while ((a % b) > 0) {
|
|
R = a % b;
|
|
a = b;
|
|
b = R;
|
|
}
|
|
return b;
|
|
}
|
|
```
|
|
|
|
شفرة جافا سكريبت لتنفيذ GCD باستخدام Recursion-
|
|
|
|
```javascript
|
|
function gcd(a, b) {
|
|
if (b == 0)
|
|
return a;
|
|
else
|
|
return gcd(b, (a % b));
|
|
}
|
|
```
|
|
|
|
يمكنك أيضًا استخدام خوارزمية Euclidean للعثور على GCD لأكثر من رقمين. نظرًا لأن GCD هي علاقة ارتباطية ، فإن العملية التالية صالحة - `GCD(a,b,c) == GCD(GCD(a,b), c)`
|
|
|
|
احسب GCD من أول رقمين ، ثم ابحث عن GCD للنتيجة والعدد التالي. مثال: `GCD(203,91,77) == GCD(GCD(203,91),77) == GCD(7, 77) == 7`
|
|
|
|
يمكنك العثور على GCD للأرقام `n` بالطريقة نفسها. |