freeCodeCamp/guide/spanish/algorithms/greatest-common-divisor-euclidean/index.md

title, localeTitle

title	localeTitle
Greatest Common Divisor Euclidean	El mayor divisor común euclidiano

El mayor divisor común euclidiano

Para este tema, debe conocer primero el Divisor común más grande (GCD) y la operación MOD.

El divisor común más grande (GCD)

El GCD de dos o más enteros es el entero más grande que divide cada uno de los enteros de tal manera que su resto es cero.

Ejemplo-
GCD de 20, 30 = 10 (10 es el número más grande que divide 20 y 30 con el resto como 0)
GCD de 42, 120, 285 = 3 (3 es el número más grande que divide a 42, 120 y 285 con el resto como 0)

Operación "mod"

La operación de modificación le da el resto cuando se dividen dos enteros positivos. Lo escribimos como sigue:
A mod B = R

Esto significa que dividir A por B le da el resto R, esto es diferente de la operación de división que le da el cociente.

Ejemplo-
7 mod 2 = 1 (Dividir 7 por 2 da el resto 1)
42 mod 7 = 0 (Dividir 42 por 7 da el resto 0)

Con los dos conceptos anteriores entendidos, comprenderá fácilmente el Algoritmo Euclidiano.

Algoritmo euclidiano para el divisor común más grande (GCD)

El algoritmo euclidiano encuentra el GCD de 2 números.

Comprenderás mejor este algoritmo viéndolo en acción. Suponiendo que desea calcular el GCD de 1220 y 516, apliquemos el algoritmo euclídeo -

Suponiendo que desea calcular el GCD de 1220 y 516, apliquemos el algoritmo euclídeo -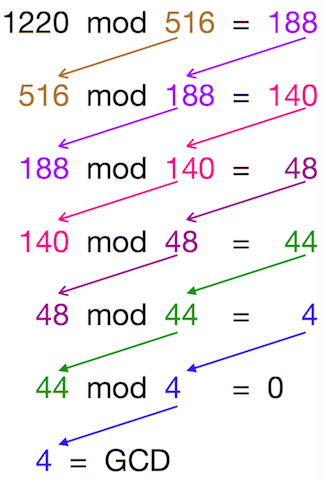

Pseudo Código del algoritmo
Paso 1: Sean a, b los dos números
Paso 2: a mod b = R
Paso 3: Deje que a = b y b = R
Paso 4: repita los pasos 2 y 3 hasta que a mod b sea ​​mayor que 0
Paso 5: GCD = b
Paso 6: Finalizar

Código Javascript para realizar GCD-

function gcd(a, b) { 
  var R; 
  while ((a % b) > 0)  { 
    R = a % b; 
    a = b; 
    b = R; 
  } 
  return b; 
 } 

Código Javascript para realizar GCD usando Recursion-

function gcd(a, b) { 
  if (b == 0) 
    return a; 
  else 
    return gcd(b, (a % b)); 
 } 

También puede usar el algoritmo euclídeo para encontrar GCD de más de dos números. Como GCD es asociativo, la siguiente operación es válida: GCD(a,b,c) == GCD(GCD(a,b), c)

Calcule el GCD de los dos primeros números, luego encuentre el GCD del resultado y el siguiente número. Ejemplo: GCD(203,91,77) == GCD(GCD(203,91),77) == GCD(7, 77) == 7

Puedes encontrar GCD de n números de la misma manera.