2.5 KiB
title
| title |
|---|
| Dynamic Programming |
Dynamic Programming
Dynamic Programming(DP) is a programming technique for solving problems where the computations of its subproblems overlap: you write your program in a way that avoids recomputing already solved problems. This technique is usually applied in conjunction with memoization which is an optimization technique where you cache previously computed results, and return the cached result when the same computation is needed again.
An example with Fibonacci's series which is defined as:
F(N) = F(N-1) + F(N-2)
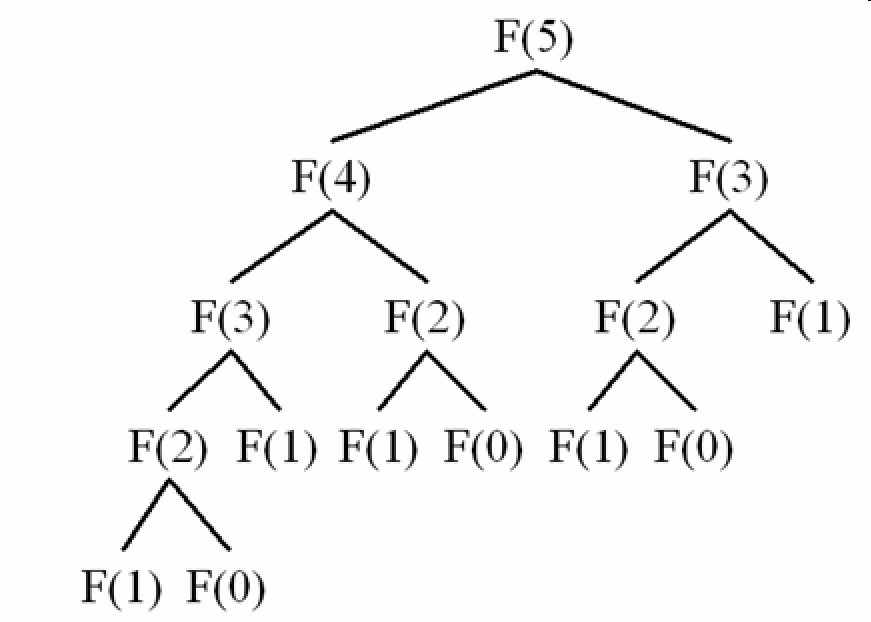
This is the tree to find F(5):
To compute F(5), the recursive method will compute the same value multiple times
For example:
F(0) is called 3 times F(1) is called 4 times F(2) is called 3 times F(3) is called 2 times
Recursive approach:
def fib(n):
if n <= 1:
return n
return fib(n-1) + fib(n-2)
For F(5), this solution will generate the calls depicted in the image above, running in O(2^N).
Here is an optimised solution which uses DP and memoization:
lookup = {1 : 1, 2 : 1} # Create a lookup-table (a map) inizialized with the first 2 Fibonacci's numbers
def fib(n):
if n in lookup: # If n is already computed
return n # Return the previous computed solution
else:
lookup[n] = fib(n-1) + fib(n-2) # Else, do the recursion.
return lookup[n]
Caching computed solutions in a lookup table, and querying it before going for recursion will let the program have a running time of O(N).
Tabulation vs Memoization
In addition to memoization (used in the previous example), there is also tabulation, which uses a bottom-up approach rather than memoization's top-down approach. Tabulation always tabulates every potential value, while memoization only calculates, or memoizes, the needed values. Tabulation avoids any recursion, however, so both are useful for different situations. Read more about tabulation vs. memoization here.
More Information:
What is dynamic programming on StackOverflow