gaspersic/freeCodeCamp
1
0
Fork 0
Code Issues Pull Requests Projects Releases Wiki Activity
Files
d53a457fc21897c205280fb790c3e60b454015ce
freeCodeCamp/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-138-special-isosceles-triangles.md

1.5 KiB
Raw Blame History

id, title, challengeType, forumTopicId, dashedName
id title challengeType forumTopicId dashedName
5900f3f61000cf542c50ff09 Problema 138: Triângulos isósceles especiais 5 301766 problem-138-special-isosceles-triangles

--description--

Considere o triângulo isósceles com o comprimento de base, b = 16, e os lados iguais, L = 17.

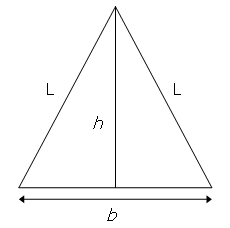
triângulo isósceles com lados chamados de L - dois lados com o mesmo comprimento e a base do triângulo chamada de b. A altura do triângulo é chamada de h e vai da base do triângulo ao ângulo entre os lados L

Usando o teorema de Pitágoras, pode ser visto que a altura do triângulo, h = \sqrt{{17}^2 - 8^2} = 15, que é uma unidade menor que o comprimento da base.

Com b = 272 e L = 305, obtemos h = 273, que é um a mais do que o comprimento da base, e este é o segundo menor triângulo isósceles com a propriedade h = b ± 1.

Encontre \sum{L} para os doze menores triângulos isósceles para os quais h = b ± 1 e b, L são números inteiros positivos.

--hints--

isoscelesTriangles() deve retornar 1118049290473932.

assert.strictEqual(isoscelesTriangles(), 1118049290473932);

--seed--

--seed-contents--

function isoscelesTriangles() {

  return true;
}

isoscelesTriangles();

--solutions--

// solution required