1.7 KiB
1.7 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4621000cf542c50ff75 | Problema 246: Tangentes de uma elipse | 5 | 301893 | problem-246-tangents-to-an-ellipse |
--description--
Uma definição para uma elipse é:
Dado um círculo c com centro M e raio r, além de um ponto G tal que d(G, M) < r, o local dos pontos que estão equidistantes de c e G formam uma elipse.
A construção dos pontos da elipse é mostrada abaixo.
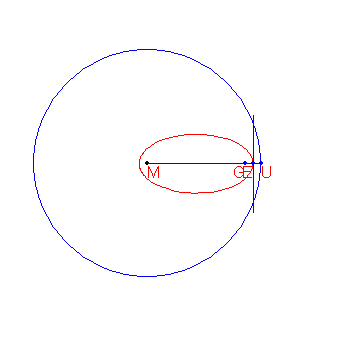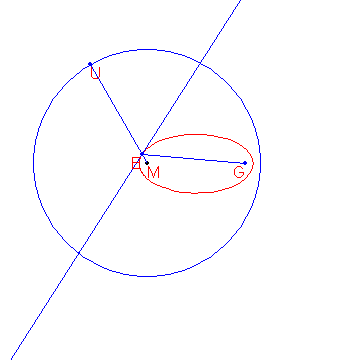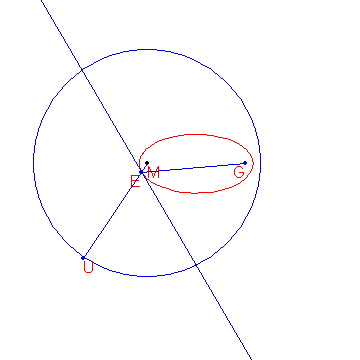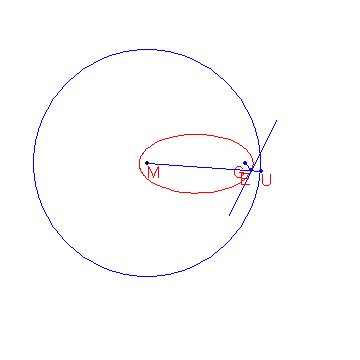
São dados os pontos M(-2000, 1500) e G(8000, 1500).
Também é dado o círculo c com centro M e raio 15.000.
A localidade dos pontos que estão equidistantes de G e c forma uma elipse e.
De um ponto P fora de e as duas tangentes t_1 e t_2 da elipse são desenhadas.
Considere os pontos em que t_1 e t_2 tocam a elipse como R e S.
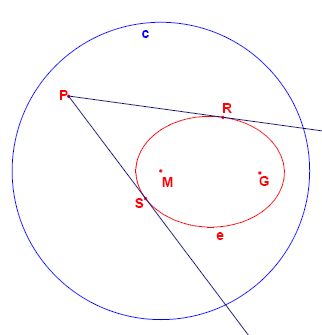
Para quantos pontos da rede P é um ângulo RPS maior que 45°?
--hints--
tangentsToAnEllipse() deve retornar 810834388.
assert.strictEqual(tangentsToAnEllipse(), 810834388);
--seed--
--seed-contents--
function tangentsToAnEllipse() {
return true;
}
tangentsToAnEllipse();
--solutions--
// solution required