freeCodeCamp/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-256-tatami-free-rooms.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f46c1000cf542c50ff7e	Problema 256: Cômodos sem tatami	5	301904	problem-256-tatami-free-rooms

--description--

Tatamis são tapetes retangulares, usados para cobrir completamente o piso de um cômodo, sem sobreposição.

Assumindo que o único tipo de tatami disponível tem dimensões de 1×2, existem, obviamente, algumas limitações quanto à forma e tamanho dos cômodos que podem ser cobertos.

Para esse problema, consideramos apenas cômodos retangulares com dimensões inteiras a, b e tamanho s = a \times b. Usamos o termo 'tamanho' para indicar a área de superfície do chão do cômodo, e — sem perda de generalidade — adicionamos a condição de que a ≤ b.

Há uma regra a seguir quando se monta o tatami: não pode haver pontos onde se encontrem cantos de quatro tapetes diferentes. Por exemplo, considere as duas disposições abaixo para um cômodo de 4×4:

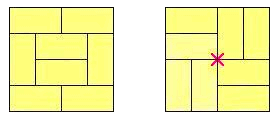
O arranjo da esquerda é aceitável, enquanto o da direita não é: um "X" vermelho no meio, marca o ponto onde quatro tatamis se encontram.

Devido a esta regra, alguns cômodos de mesmo tamanho não podem ser cobertos por tatami: damos a eles o nome de cômodos sem tatami. Além disso, definimos T(s) como o número de cômodos sem tatami no tamanho s.

O menor cômodo sem tatami tem tamanho s = 70 e dimensões de 7×10. Todos os outros cômodos do tamanho s = 70 podem ser cobertos com tatami; eles são: 1×70, 2×35 e 5×14. Portanto, T(70) = 1.

Da mesma forma, podemos verificar que T(1320) = 5 porque há exatamente 5 cômodos sem tatami s = 1320: 20×66, 22×60, 24×55, 30×44 e 33×40. Na verdade, s = 1320 é o menor tamanho de cômodo s para o qual T(s) = 5.

Encontre o menor tamanho de cômodo s para o qual T(s) = 200.

--hints--

tatamiFreeRooms() deve retornar 85765680.

assert.strictEqual(tatamiFreeRooms(), 85765680);

--seed--

--seed-contents--

function tatamiFreeRooms() {

  return true;
}

tatamiFreeRooms();

--solutions--

// solution required