1.5 KiB
1.5 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f46e1000cf542c50ff80 | Problema 257: Bissetores angulares | 5 | 301905 | problem-257-angular-bisectors |
--description--
Você recebe um triângulo com o comprimento dos lados de números inteiros ABC com lados a ≤ b ≤ c. (AB = c, BC = a e AC = b).
Os bissetores angulares do triângulo cruzam os lados nos pontos E, F e G (veja a imagem abaixo).
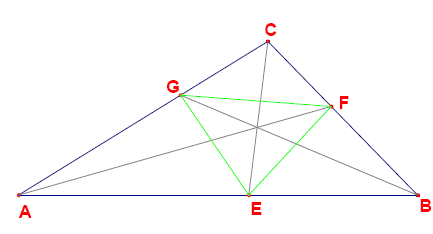
Os segmentos EF, EG e FG particionam o triângulo ABC em quatro triângulos menores: AEG, BFE, CGF e EFG. Pode ser provado que, para cada um desses quatro triângulos, a razão \frac{\text{área}(ABC)}{\text{área}(\text{subtriângulo})} é racional. No entanto, existem triângulos para os quais algumas ou todas estas razões são inteiras.
Quantos triângulos ABC com o perímetro ^\\100.000.000 existem para que a razão \frac{\text{área}(ABC)}{\text{área}(AEG)} seja integral?
--hints--
angularBisectors() deve retornar 139012411.
assert.strictEqual(angularBisectors(), 139012411);
--seed--
--seed-contents--
function angularBisectors() {
return true;
}
angularBisectors();
--solutions--
// solution required