1.7 KiB
1.7 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4931000cf542c50ffa6 | Problema 295: Orifícios lenticulares | 5 | 301947 | problem-295-lenticular-holes |
--description--
Chamamos a área convexa criada no cruzamento de dois círculos de um orifício lenticular se:
- Os centros de ambos os círculos estão em pontos da rede.
- Os dois círculos se cruzam em dois pontos de da rede distintos.
- O interior da área convexa criada pelos dois os círculos não contém pontos da rede.
Considere os círculos:
\begin{align} & C_0: x^2 + y^2 = 25 \\\\ & C_1: {(x + 4)}^2 + {(y - 4)}^2 = 1 \\\\ & C_2: {(x - 12)}^2 + {(y - 4)}^2 = 65 \end{align}
Os círculos C_0, C_1 e C_2 estão desenhados na imagem abaixo.
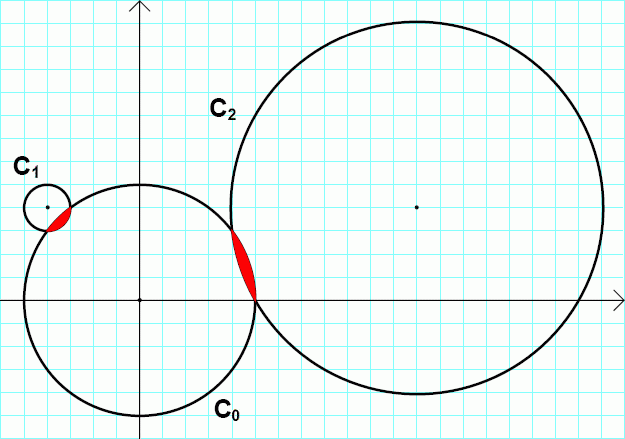
C_0 e C_1 formam um orifício lenticular, assim como C_0 e C_2.
Chamamos de par ordenado de números reais positivos (r_1, r_2) um par lenticular se existirem dois círculos com raio r_1 e r_2 que formem um orifício lenticular. Podemos verificar que (1, 5) e (5, \sqrt{65}) são os pares lenticulares do exemplo acima.
Considere L(N) como o número de pares lenticulares distintos (r_1, r_2) para os quais 0 < r_1 ≤ r_2 ≤ N. Podemos verificar que L(10) = 30 e L(100) = 3442.
Encontre L(100.000).
--hints--
lenticularHoles() deve retornar 4884650818.
assert.strictEqual(lenticularHoles(), 4884650818);
--seed--
--seed-contents--
function lenticularHoles() {
return true;
}
lenticularHoles();
--solutions--
// solution required