2.6 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4a71000cf542c50ffb9 | Problema 314: O rato na lua | 5 | 301970 | problem-314-the-mouse-on-the-moon |
--description--
A lua foi liberada e terrenos podiam ser obtidos gratuitamente, mas tem uma pegadinha. É preciso construir um muro ao redor do terreno de que nos apropriamos. Construir um muro na lua é caro. Todos os países receberam um dote de 500 m por 500 m quadrados, mas eles só possuem as áreas que eles cercarem com o muro. 251001 postes foram colocados em uma grade retangular com um espaçamento de 1 metro. O muro deve ser uma série fechada de linhas retas, cada linha indo de um poste a outro.
Os países maiores construíram, é claro, uma parede de 2000 metros que inclui toda a área de 250 000 \text{m}^2. O Ducado do Grande Fenwick tem um orçamento mais apertado. Ele pediu para você (o Programador Real) calcular qual formato obteria a melhor proporção máxima de \frac{\text{área cercada}}{\text{comprimento do muro}}.
Você já fez cálculos preliminares em uma folha de papel. Para um muro de 2000 metros cercando a área de 250 000 \text{m}^2, a proporção de \frac{\text{área cercada}}{\text{comprimento do muro}} é de 125.
Embora não seja permitido, mas para ter uma ideia se isto era melhor: se você colocar um círculo dentro da área quadrada tocando os quatro lados, a área será igual a π \times {250}^2 \text{m}^2 e o perímetro será π \times 500 \text{m}, então a proporção \frac{\text{área cercada}}{\text{comprimento do muro}} também será 125.
No entanto, se você cortar do quadrados qyatro triângulos com lados 75 m, 75 m e 75\sqrt{2} m, a área total se torna 238750 \text{m}^2 e o perímetro se torna 1400 + 300\sqrt{2} m. Então, isso dá uma proporção de \frac{\text{área cercada}}{\text{comprimento do muro}} de 130,87, o que é significativamente melhor.
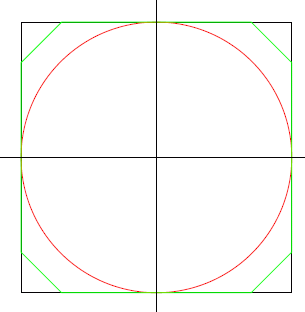
Encontre a proporção máxima de \frac{\text{área cercada}}{\text{comprimento do muro}}. Arredonde sua resposta para até 8 casas decimais usando o formato abc.defghijk.
--hints--
theMouseOnTheMoon() deve retornar 132.52756426.
assert.strictEqual(theMouseOnTheMoon(), 132.52756426);
--seed--
--seed-contents--
function theMouseOnTheMoon() {
return true;
}
theMouseOnTheMoon();
--solutions--
// solution required