2.1 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4d91000cf542c50ffeb | Problema 363: Curva de Bézier | 5 | 302024 | problem-363-bzier-curves |
--description--
Uma curva cúbica de Bézier é definida por quatro pontos: P_0, P_1, P_2 e P_3.
A curva é construída da seguinte forma:
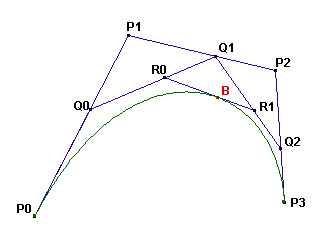
Nos segmentos P_0P_1, P_1P_2 e P_2P_3 os pontos Q_0,$Q_1$ e Q_2 estão desenhados tal que \frac{P_0Q_0}{P_0P_1} = \frac{P_1Q_1}{P_1P_2} = \frac{P_2Q_2}{P_2P_3} = t, com t em [0,1].
Nos segmentos Q_0Q_1 e Q_1Q_2 os pontos R_0 e R_1 estão desenhados, tal que \frac{Q_0R_0}{Q_0Q_1} = \frac{Q_1R_1}{Q_1Q_2} = t pelo mesmo valor de t.
No segmento R_0R_1 o ponto B é desenhado de forma que \frac{R_0B}{R_0R_1} = t tenha o mesmo valor de t.
A curva de Bézier definida pelos pontos P_0, P_1, P_2, P_3 é a localidade de B pois Q_0 ocupa todas as posições possíveis no segmento P_0P_1. Observe que, para todos os pontos, o valor de t é o mesmo.
A partir da construção, fica claro que a curva de Bézier será tangente aos segmentos P_0P_1 em P_0 e P_2P_3 em P_3.
Uma curva de Bézier cúbica com P_0 = (1, 0), P_1 = (1, v), P_2 = (v, 1) e P_3 = (0, 1) é usada para aproximar um quarto de círculo. O valor v > 0 foi escolhido de modo que a área circundada pelas linhas OP_0, OP_3 e a curva é igual a \frac{π}{4} (a área do quarto de círculo).
Qual a porcentagem do comprimento da curva que difere do comprimento do quarto de círculo? Ou seja, se L for o comprimento da curva, calcule 100 × \displaystyle\frac{L – \frac{π}{2}}{\frac{π}{2}}. Dê sua resposta arredondada para 10 casas depois da vírgula.
--hints--
bezierCurves() deve retornar 0.0000372091.
assert.strictEqual(bezierCurves(), 0.0000372091);
--seed--
--seed-contents--
function bezierCurves() {
return true;
}
bezierCurves();
--solutions--
// solution required