2.3 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f5381000cf542c51004b | Problema 460: Uma formiga em movimento | 5 | 302135 | problem-460-an-ant-on-the-move |
--description--
No plano euclideano, uma formiga viaja do ponto A(0, 1) ao ponto B(d, 1) para um número inteiro d.
Em cada passo, a formiga no ponto (x_0, y_0) escolhe um dos pontos da rede (x_1, y_1) que satisfaça x_1 ≥ 0 e y_1 ≥ 1 e vai direto para (x_1, y_1) com velocidade vetorial constante v. O valor de v depende de y_0 e y_1 da seguinte forma:
- Se
y_0 = y_1, o valor devé igual ay_0. - Se
y_0 ≠ y_1, o valor devé igual a\frac{y_1 - y_0}{\ln y_1 - \ln y_0}.
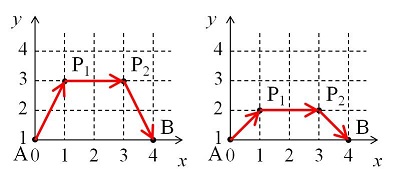
A imagem á esquerda é um dos possíveis caminhos para d = 4. Primeiro, a formiga vai de A(0, 1) para P_1(1, 3) a uma velocidade de \frac{3 - 1}{\ln 3 - \ln 1} ≈ 1.8205. Então, o tempo necessário é de \frac{\sqrt{5}}{1.820} ≈ 1.2283.
De P_1(1, 3) para P_2(3, 3), a formiga viaja à uma velocidade vetorial de 3. Então, o tempo necessário é \frac{2}{3} ≈ 0.6667. De P_2(3, 3) para B(4, 1), a formiga viaja à uma velocidade vetorial de \frac{1 - 3}{\ln 1 - \ln 3} ≈ 1.8205. Então, o tempo necessário será \frac{\sqrt{5}}{1.8205} ≈ 1.2283.
Dessa forma, o tempo total necessário é de 1.2283 + 0.6667 + 1.2283 = 3.1233.
A imagem à direita é outro caminho. O tempo total necessário é calculado por 0.98026 + 1 + 0.98026 = 2.96052. Isso mostra que esse é o caminho mais rápido para d = 4.
Considere F(d) como o tempo total necessário se a formiga escolher o caminho mais rápido. Por exemplo, F(4) ≈ 2.960.516.287. Podemos verificar que F(10) ≈ 4.668.187.834 e que F(100) ≈ 9.217.221.972.
Calcule F(10.000). Dê sua resposta arredondada para nove casas decimais.
--hints--
antOnTheMove() deve retornar 18.420738199.
assert.strictEqual(antOnTheMove(), 18.420738199);
--seed--
--seed-contents--
function antOnTheMove() {
return true;
}
antOnTheMove();
--solutions--
// solution required