freeCodeCamp/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-86-cuboid-route.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f3c31000cf542c50fed5	Problema 86: Rota de um cuboide	5	302200	problem-86-cuboid-route

--description--

Uma aranha, S, está no canto de uma sala em formato de cubo, medindo 6 por 3, e uma mosca, F, fica no canto oposto. Ao passear pelas superfícies da sala, a menor distância de "linha reta" entre S e F é 10 e o caminho é mostrado no diagrama.

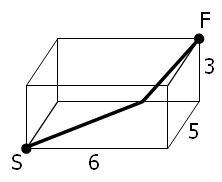
No entanto, há até três candidatos a caminhos "mais curtos" para qualquer cuboide dado. O caminho mais curto nem sempre tem o tamanho expresso em números inteiros.

Pode-se mostrar aqui que há exatamente 2060 cubos distintos, ignorando rotações, com dimensões inteiras, até um tamanho máximo de M por M por M, para os quais a rota mais curta tem comprimento inteiro quando M = 100. Este é o menor valor de M para o qual o número de soluções excede duas mil. O número de soluções quando M = 99 é 1975.

Encontre o menor valor de M, de modo que o número de soluções exceda n.

--hints--

cuboidRoute(2000) deve retornar um número.

assert(typeof cuboidRoute(2000) === 'number');

cuboidRoute(2000) deve retornar 100.

assert.strictEqual(cuboidRoute(2000), 100);

cuboidRoute(25000) deve retornar 320.

assert.strictEqual(cuboidRoute(25000), 320);

cuboidRoute(500000) deve retornar 1309.

assert.strictEqual(cuboidRoute(500000), 1309);

cuboidRoute(1000000) deve retornar 1818.

assert.strictEqual(cuboidRoute(1000000), 1818);

--seed--

--seed-contents--

function cuboidRoute(n) {

  return true;
}

cuboidRoute(2000);

--solutions--

function cuboidRoute(n) {
  // Based on https://www.mathblog.dk/project-euler-86-shortest-path-cuboid/
  function getLength(a, b) {
    return Math.sqrt(a ** 2 + b ** 2);
  }

  let M = 2;
  let counter = 0;

  while (counter < n) {
    M++;
    for (let baseHeightWidth = 3; baseHeightWidth <= 2 * M; baseHeightWidth++) {
      const pathLength = getLength(M, baseHeightWidth);
      if (Number.isInteger(pathLength)) {
        if (baseHeightWidth <= M) {
          counter += Math.floor(baseHeightWidth / 2);
        } else {
          counter += 1 + M - Math.floor((baseHeightWidth + 1) / 2);
        }
      }
    }
  }

  return M;
}