21 lines
1.5 KiB
Markdown
21 lines
1.5 KiB
Markdown
---
|
|
title: Piecewise Functions Graphs
|
|
localeTitle: Funciones de trozos gráficos
|
|
---
|
|
## Funciones de trozos gráficos
|
|
|
|
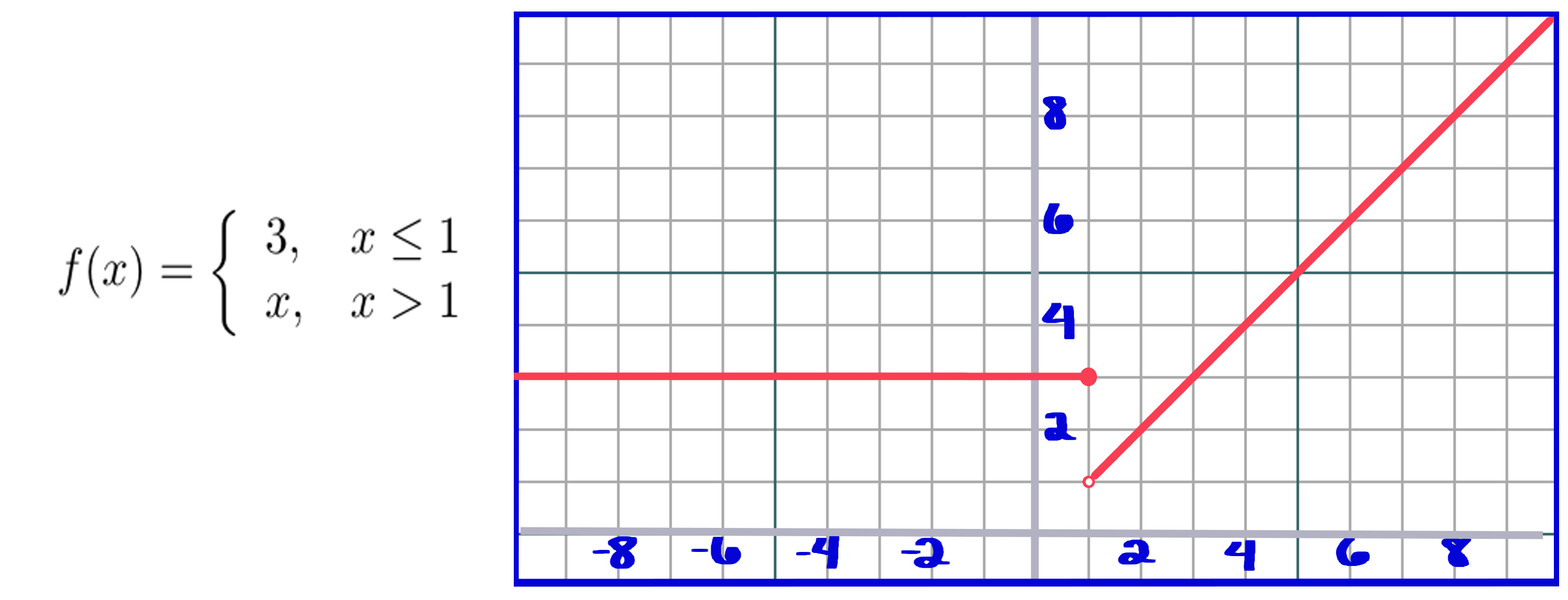
Las funciones por partes se definen de manera diferente para diferentes intervalos de `x` . Para encontrar `y` , usas `x` para ver en qué intervalo está. Veamos una función simple por tramos y su gráfica.
|
|
|
|
|
|
|
|
Puedes ver que cuando `x` es menor o igual que 1, `y` es igual a 3, y cuando `x` es mayor que 1, `y` es igual a x. Es casi como si las funciones por partes se crearan combinando diferentes funciones en una.
|
|
|
|
|
|
|
|
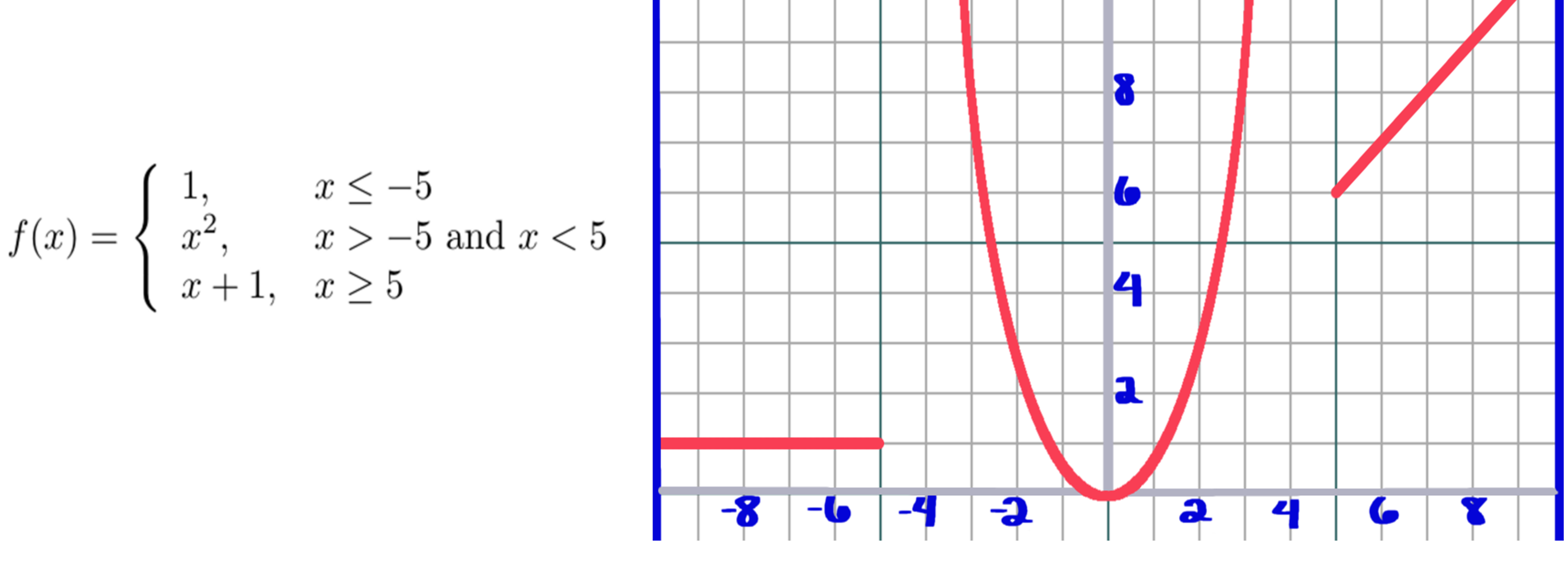
En el gráfico anterior puede ver que `x` cuadrado podría ser una función independiente que se definiría para todos los números reales. En su lugar, hemos definido nuestra función por partes, de modo que solo los valores de `x` que son mayores que -5 y menores que 5 se ingresan en `x` cuadrado. Observe que este gráfico parece tener dos "líneas de límite" en `x = -5` y `x = 5` , y el primer gráfico tiene una "línea de límite" en `x = 1` .
|
|
|
|
### Funciones continuas / no continuas por partes
|
|
|
|
¿Cómo puedes saber si una función particular por partes es continua? Veamos un par de ejemplos.
|
|
|
|
 |