* fix: imgur to s3 for russian guide without conflict (cherry picked from commit ac90750e36b0dd1fe508c69a2277b75be48e4b95) * fix: remove extra links Co-Authored-By: Randell Dawson <5313213+RandellDawson@users.noreply.github.com> * fix: revert unrelated changes * fix: revert changes
75 lines
3.6 KiB
Markdown
75 lines
3.6 KiB
Markdown
---
|
||
title: Greatest Common Divisor Euclidean
|
||
localeTitle: Величайший общий делитель Евклидов
|
||
---
|
||
## Величайший общий делитель Евклидов
|
||
|
||
Для этой темы вы должны сначала знать о Величайшем общем делителе (GCD) и операции MOD.
|
||
|
||
#### Самый большой общий делитель (GCD)
|
||
|
||
GCD двух или более целых чисел является наибольшим целым числом, которое делит каждое из целых чисел таким образом, что их остаток равен нулю.
|
||
|
||
Пример-
|
||
GCD 20, 30 = 10 _(10 - наибольшее число, которое делит 20 и 30 с остатком в 0)_
|
||
GCD 42, 120, 285 = 3 _(3 - наибольшее число, которое делит 42, 120 и 285 с остатком как 0)_
|
||
|
||
#### Операция "mod"
|
||
|
||
Операция mod дает вам остаток, когда разделяются два положительных целых числа. Мы пишем его следующим образом:
|
||
`A mod B = R`
|
||
|
||
Это означает, что деление A на B дает вам остаток R, это отличается от операции деления, которая дает вам коэффициент.
|
||
|
||
Пример-
|
||
7 mod 2 = 1 _(Разделение 7 на 2 дает остаток 1)_
|
||
42 mod 7 = 0 _(Разделение 42 на 7 дает остаток 0)_
|
||
|
||
С учетом этих двух понятий вы легко поймете Евклидовы алгоритмы.
|
||
|
||
### Евклидовой алгоритм для наибольшего общего делителя (GCD)
|
||
|
||
В евклидовом алгоритме найден GCD из 2 чисел.
|
||
|
||
Вы лучше поймете этот алгоритм, увидев его в действии. Предполагая, что вы хотите вычислить GCD 1220 и 516, давайте применим Евклидовой алгоритм-
|
||
|
||
Предполагая, что вы хотите вычислить GCD 1220 и 516, давайте применим Евклидовой алгоритм- 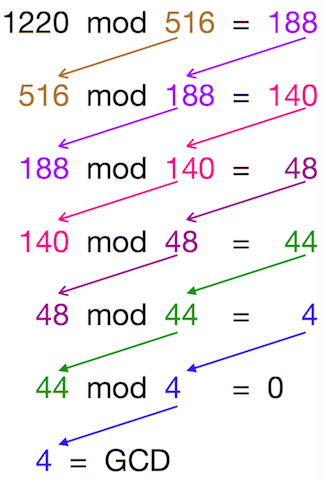
|
||
|
||
Псевдокод алгоритма-
|
||
Шаг 1: **Пусть `a, b` - два числа**
|
||
Шаг 2: **`a mod b = R`**
|
||
Шаг 3: **Пусть `a = b` и `b = R`**
|
||
Шаг 4: **Повторите шаги 2 и 3 до тех пор, пока `a mod b` станет больше 0**
|
||
Шаг 5: **GCD = b**
|
||
Шаг 6: Закончите
|
||
|
||
Код Javascript для выполнения GCD-
|
||
|
||
```javascript
|
||
function gcd(a, b) {
|
||
var R;
|
||
while ((a % b) > 0) {
|
||
R = a % b;
|
||
a = b;
|
||
b = R;
|
||
}
|
||
return b;
|
||
}
|
||
```
|
||
|
||
Код Javascript для выполнения GCD с использованием рекурсивно-
|
||
|
||
```javascript
|
||
function gcd(a, b) {
|
||
if (b == 0)
|
||
return a;
|
||
else
|
||
return gcd(b, (a % b));
|
||
}
|
||
```
|
||
|
||
Вы также можете использовать Евклидовой алгоритм для поиска GCD более двух чисел. Поскольку GCD ассоциативен, справедлива следующая операция: `GCD(a,b,c) == GCD(GCD(a,b), c)`
|
||
|
||
Вычислите GCD первых двух чисел, затем найдите GCD результата и следующее число. Пример - `GCD(203,91,77) == GCD(GCD(203,91),77) == GCD(7, 77) == 7`
|
||
|
||
Вы можете найти GCD из `n` чисел таким же образом. |