269 lines
16 KiB
Markdown
269 lines
16 KiB
Markdown
---
|
||
title: Binary Search Trees
|
||
localeTitle: Деревья двоичного поиска
|
||
---
|
||
## Деревья двоичного поиска
|
||
|
||
|
||
|
||
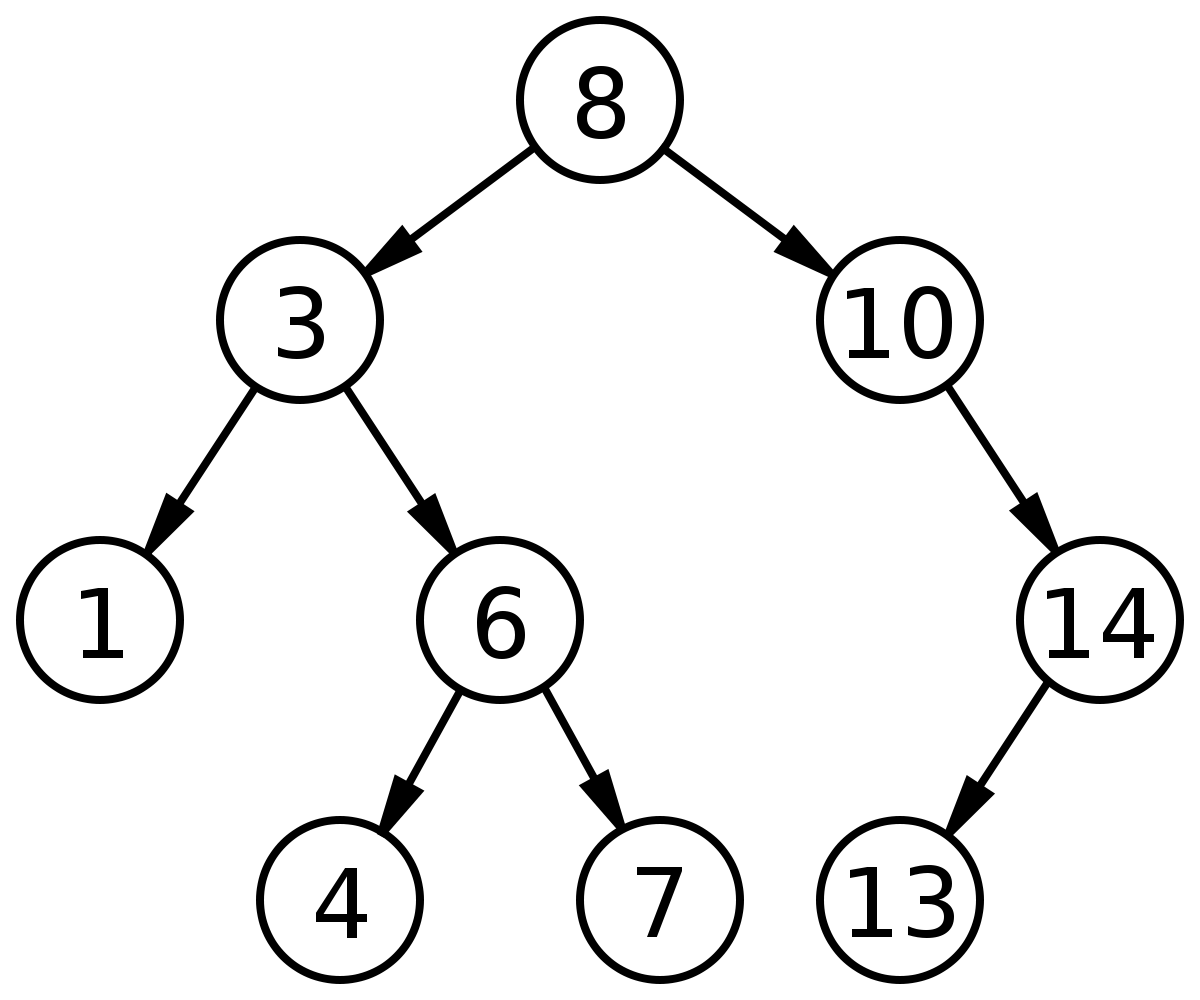
Дерево представляет собой структуру данных, состоящую из узлов, которые имеют следующие характеристики:
|
||
|
||
1. Каждое дерево имеет корневой узел (вверху), имеющий некоторое значение.
|
||
2. Корневой узел имеет ноль или более дочерних узлов.
|
||
3. Каждый дочерний узел имеет ноль или более дочерних узлов и т. Д. Это создает поддерево в дереве. Каждый узел имеет свое собственное поддерево, состоящее из его детей и их детей и т. Д. Это означает, что каждый узел сам по себе может быть деревом.
|
||
|
||
Двоичное дерево поиска (BST) добавляет эти две характеристики:
|
||
|
||
1. Каждый узел имеет максимум до двух детей.
|
||
2. Для каждого узла значения его левых узлов-потомков меньше, чем у текущего узла, который, в свою очередь, меньше, чем правые узлы-потомки (если они есть).
|
||
|
||
BST построен на идее алгоритма [бинарного поиска](https://guide.freecodecamp.org/algorithms/search-algorithms/binary-search) , который позволяет быстро находить, вставлять и удалять узлы. Способ их настройки означает, что в среднем каждое сравнение позволяет операциям пропускать около половины дерева, так что каждый поиск, вставка или удаление занимает время, пропорциональное логарифму количества элементов, хранящихся в дереве, `O(log n)` . Однако иногда может произойти худший случай, когда дерево не сбалансировано, а временная сложность `O(n)` для всех трех этих функций. Вот почему самобалансирующиеся деревья (AVL, red-black и т. Д.) Намного эффективнее базового BST.
|
||
|
||
**Пример худшего сценария:** это может произойти, когда вы добавляете узлы, которые _всегда_ больше, чем узел (родительский), то же самое может произойти, когда вы всегда добавляете узлы со значениями ниже своих родителей.
|
||
|
||
### Основные операции на BST
|
||
|
||
* Create: создает пустое дерево.
|
||
* Вставить: вставить узел в дерево.
|
||
* Поиск: поиск узла в дереве.
|
||
* Удалить: удаляет узел из дерева.
|
||
|
||
#### Создайте
|
||
|
||
Сначала создается пустое дерево без каких-либо узлов. Переменная / идентификатор, который должен указывать на корневой узел, инициализируется значением `NULL` .
|
||
|
||
#### Поиск
|
||
|
||
Вы всегда начинаете искать дерево в корневом узле и спускаетесь оттуда. Вы сравниваете данные в каждом узле с тем, который вы ищете. Если сравниваемый узел не совпадает, вы либо переходите к правильному ребенку, либо к левому ребенку, что зависит от результата следующего сравнения: если узел, который вы ищете, меньше, чем тот, с которым вы сравнивали его, вы переходите к левому ребенку, иначе (если он больше) вы переходите к правильному ребенку. Зачем? Поскольку BST структурирован (согласно его определению), что правильный ребенок всегда больше родителя, а левый ребенок всегда меньше.
|
||
|
||
#### Вставить
|
||
|
||
Он очень похож на функцию поиска. Вы снова начинаете с корня дерева и возвращаетесь рекурсивно, ища подходящее место для вставки нашего нового узла так же, как описано в функции поиска. Если узел с тем же значением уже находится в дереве, вы можете выбрать либо вставить дубликат, либо нет. Некоторые деревья допускают дубликаты, некоторые - нет. Это зависит от определенной реализации.
|
||
|
||
#### делеция
|
||
|
||
Есть три случая, которые могут произойти, когда вы пытаетесь удалить узел. Если это так,
|
||
|
||
1. Нет поддерева (без детей): этот самый простой. Вы можете просто удалить узел без каких-либо дополнительных действий.
|
||
2. Одно поддерево (один ребенок): вы должны убедиться, что после удаления узла его дочерний элемент затем подключается к родительскому элементу удаленного узла.
|
||
3. Два поддерева (двое детей): вы должны найти и заменить узел, который хотите удалить, с его преемником (letfmost node в правом поддереве).
|
||
|
||
Сложность времени для создания дерева - `O(1)` . Сложность времени для поиска, вставки или удаления узла зависит от высоты дерева `h` , поэтому худшим случаем является `O(h)` .
|
||
|
||
#### Предшественник узла
|
||
|
||
Предшественники можно охарактеризовать как узел, который появится прямо перед узлом, в котором вы сейчас находитесь. Чтобы найти предшественника текущего узла, посмотрите на правый / самый большой листовой узел в левом поддереве.
|
||
|
||
#### Преемник узла
|
||
|
||
Преемники можно охарактеризовать как узел, который появится сразу после узла, в котором вы сейчас находитесь. Чтобы найти преемника текущего узла, посмотрите на самый левый или самый маленький листовой узел в правом поддереве.
|
||
|
||
### Специальные типы BT
|
||
|
||
* отвал
|
||
* Красно-черное дерево
|
||
* В-дерево
|
||
* Splay tree
|
||
* N-арное дерево
|
||
* Trie (дерево Radix)
|
||
|
||
### время выполнения
|
||
|
||
**Структура данных: массив**
|
||
|
||
* Наихудшая производительность: `O(log n)`
|
||
* Лучшая производительность: `O(1)`
|
||
* Средняя производительность: `O(log n)`
|
||
* Сложная сложность пространства: `O(1)`
|
||
|
||
Где `n` - количество узлов в BST.
|
||
|
||
### Внедрение BST
|
||
|
||
Вот определение для узла BST, имеющего некоторые данные, ссылающиеся на его левый и правый дочерние узлы.
|
||
|
||
```c
|
||
struct node {
|
||
int data;
|
||
struct node *leftChild;
|
||
struct node *rightChild;
|
||
};
|
||
```
|
||
|
||
#### Операция поиска
|
||
|
||
Всякий раз, когда элемент нужно искать, начните поиск с корневого узла. Затем, если данные меньше значения ключа, выполните поиск элемента в левом поддереве. В противном случае выполните поиск элемента в правом поддереве. Следуйте одному и тому же алгоритму для каждого узла.
|
||
|
||
```c
|
||
struct node* search(int data){
|
||
struct node *current = root;
|
||
printf("Visiting elements: ");
|
||
|
||
while(current->data != data){
|
||
|
||
if(current != NULL) {
|
||
printf("%d ",current->data);
|
||
|
||
//go to left tree
|
||
if(current->data > data){
|
||
current = current->leftChild;
|
||
}//else go to right tree
|
||
else {
|
||
current = current->rightChild;
|
||
}
|
||
|
||
//not found
|
||
if(current == NULL){
|
||
return NULL;
|
||
}
|
||
}
|
||
}
|
||
return current;
|
||
}
|
||
```
|
||
|
||
#### Вставить операцию
|
||
|
||
Всякий раз, когда элемент должен быть вставлен, сначала найдите его правильное местоположение. Начните поиск с корневого узла, затем, если данные меньше значения ключа, найдите пустое место в левом поддереве и вставьте данные. В противном случае найдите пустое место в правом поддереве и вставьте данные.
|
||
|
||
```c
|
||
void insert(int data) {
|
||
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
|
||
struct node *current;
|
||
struct node *parent;
|
||
|
||
tempNode->data = data;
|
||
tempNode->leftChild = NULL;
|
||
tempNode->rightChild = NULL;
|
||
|
||
//if tree is empty
|
||
if(root == NULL) {
|
||
root = tempNode;
|
||
} else {
|
||
current = root;
|
||
parent = NULL;
|
||
|
||
while(1) {
|
||
parent = current;
|
||
|
||
//go to left of the tree
|
||
if(data < parent->data) {
|
||
current = current->leftChild;
|
||
//insert to the left
|
||
|
||
if(current == NULL) {
|
||
parent->leftChild = tempNode;
|
||
return;
|
||
}
|
||
}//go to right of the tree
|
||
else {
|
||
current = current->rightChild;
|
||
|
||
//insert to the right
|
||
if(current == NULL) {
|
||
parent->rightChild = tempNode;
|
||
return;
|
||
}
|
||
}
|
||
}
|
||
}
|
||
}
|
||
```
|
||
|
||
Двоичные деревья поиска (BST) также дают нам быстрый доступ к предшественникам и преемникам. Предшественники можно охарактеризовать как узел, который появится прямо перед узлом, в котором вы сейчас находитесь.
|
||
|
||
* Чтобы найти предшественника текущего узла, посмотрите на самый правый / самый большой листовой узел в левом поддереве. Преемники можно охарактеризовать как узел, который появится сразу после узла, в котором вы сейчас находитесь.
|
||
* Чтобы найти преемника текущего узла, посмотрите на самый левый / самый маленький листовой узел в правом поддереве.
|
||
|
||
### Давайте посмотрим на пару процедур, работающих на деревьях.
|
||
|
||
Поскольку деревья рекурсивно определены, очень часто приходится писать процедуры, которые работают на деревьях, которые сами являются рекурсивными.
|
||
|
||
Например, если мы хотим рассчитать высоту дерева, то есть высоту корневого узла, мы можем идти вперед и рекурсивно делать это, проходя через дерево. Поэтому мы можем сказать:
|
||
|
||
* Например, если у нас есть дерево nil, то его высота равна 0.
|
||
* В противном случае мы достигнем 1 плюс максимум левого дочернего дерева и правого дочернего дерева.
|
||
* Поэтому, если мы посмотрим на лист, например, эта высота будет равна 1, так как высота левого дочернего элемента равна нулю, равно 0, а высота нулевого правильного ребенка равна 0. Таким образом, максимальная величина равна 0, затем 1 плюс 0.
|
||
|
||
#### Алгоритм высоты (дерева)
|
||
```
|
||
if tree = nil:
|
||
return 0
|
||
return 1 + Max(Height(tree.left),Height(tree.right))
|
||
```
|
||
|
||
#### Вот код в C ++
|
||
```
|
||
int maxDepth(struct node* node)
|
||
{
|
||
if (node==NULL)
|
||
return 0;
|
||
else
|
||
{
|
||
int rDepth = maxDepth(node->right);
|
||
int lDepth = maxDepth(node->left);
|
||
|
||
if (lDepth > rDepth)
|
||
{
|
||
return(lDepth+1);
|
||
}
|
||
else
|
||
{
|
||
return(rDepth+1);
|
||
}
|
||
}
|
||
}
|
||
```
|
||
|
||
Мы могли бы также посмотреть на вычисление размера дерева, которое является числом узлов.
|
||
|
||
* Опять же, если у нас есть дерево nil, у нас есть нулевые узлы.
|
||
* В противном случае мы имеем число узлов в левом дочернем элементе плюс 1 для себя плюс число узлов в правом дочернем элементе. Итак, 1 плюс размер левого дерева плюс размер правильного дерева.
|
||
|
||
#### Алгоритм размера (дерева)
|
||
```
|
||
if tree = nil
|
||
return 0
|
||
return 1 + Size(tree.left) + Size(tree.right)
|
||
```
|
||
|
||
#### Вот код в C ++
|
||
```
|
||
int treeSize(struct node* node)
|
||
{
|
||
if (node==NULL)
|
||
return 0;
|
||
else
|
||
return 1+(treeSize(node->left) + treeSize(node->right));
|
||
}
|
||
```
|
||
|
||
### Соответствующие видео на канале freeCodeCamp YouTube
|
||
|
||
* [Двоичное дерево поиска](https://youtu.be/5cU1ILGy6dM)
|
||
* [Двоичное дерево поиска: обход и высота](https://youtu.be/Aagf3RyK3Lw)
|
||
|
||
### Ниже приведены общие типы двоичных деревьев:
|
||
|
||
Полное двоичное дерево / строковое двоичное дерево: двоичное дерево является полным или строгим, если каждый узел имеет ровно 0 или 2 детей.
|
||
```
|
||
18
|
||
/ \
|
||
15 30
|
||
/ \ / \
|
||
40 50 100 40
|
||
```
|
||
|
||
В полном двоичном дереве количество листовых узлов равно числу внутренних узлов плюс один.
|
||
|
||
Полное двоичное дерево: двоичное дерево является полным двоичным деревом, если все уровни полностью заполнены, за исключением, возможно, последнего уровня, а последний уровень имеет все ключи как можно дальше
|
||
```
|
||
18
|
||
/ \
|
||
15 30
|
||
/ \ / \
|
||
40 50 100 40
|
||
/ \ /
|
||
8 7 9
|
||
|
||
``` |