1.6 KiB
1.6 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f3ea1000cf542c50fefd | 問題 126: 直方体の層 | 5 | 301753 | problem-126-cuboid-layers |
--description--
寸法が 3 x 2 x 1 の直方体の表面をすべて覆うには、少なくとも 22 個の立方体が必要です。
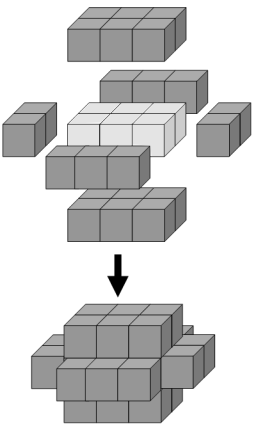
この立体に 2 層目を加える場合、表面をすべて覆うには 46 個の立方体が必要になります。さらに 3 層目では 78 個、4 層目では 118 個の立方体が必要です。
しかし、5 × 1 × 1 の直方体でも 1 層目に 22 個の立方体が必要であり、同様に、5 × 3 × 1, 7 × 2 × 1, 11 × 1 × 1 の直方体はいずれも 1 層目が 46 個の立方体からなります。
いずれか 1 つの層が n 個の立方体からなるような直方体の個数を、C(n) とします。 したがって、C(22) = 2, C(46) = 4, C(78) = 5, C(118) = 8 です。
C(n) = 10 のとき、最小の n が 154 であることが分かります。
C(n) = 1000 のとき、n の最小値を求めなさい。
--hints--
cuboidLayers() は 18522 を返す必要があります。
assert.strictEqual(cuboidLayers(), 18522);
--seed--
--seed-contents--
function cuboidLayers() {
return true;
}
cuboidLayers();
--solutions--
// solution required