Files

camperbot 5c868af2b8 chore(i18n,learn): processed translations (#44851 )

2022-01-20 20:30:18 +01:00

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f41a1000cf542c50ff2d	問題 174: 1, 2, 3, ... 種類の配置を作れる「穴あき」正方層を数え上げる	5	301809	problem-174-counting-the-number-of-hollow-square-laminae-that-can-form-one-two-three-----distinct-arrangements

--description--

輪郭が正方形であり、正方形の「穴」があり、上下対称かつ左右対称であるものを「正方層」と呼ぶことにします。

8 枚のタイルを使って作れる正方層は 1 通り (1 x 1 の穴を持つ 3 x 3) のみです。しかし、32 枚のタイルを使うと 2 通りの正方層を作成できます。

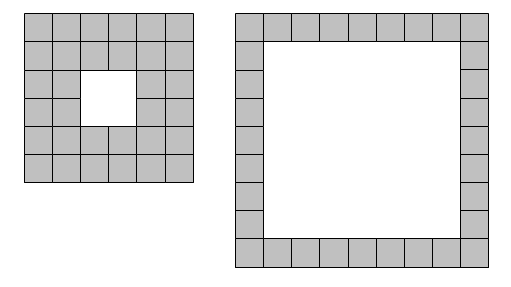
使用するタイルの枚数を t で表し、t = 8 は L(1) 型、t = 32 は L(2) 型であると表現することにします。

t が L(n) 型であるような t (≤ 1000000) の数を N(n) とします。例えば、N(15) = 832 です。

1 ≤ n ≤ 10 のとき、\sum N(n) を求めなさい。

--hints--

hollowSquareLaminaeDistinctArrangements() は 209566 を返す必要があります。

assert.strictEqual(hollowSquareLaminaeDistinctArrangements(), 209566);

function hollowSquareLaminaeDistinctArrangements() {

  return true;
}

hollowSquareLaminaeDistinctArrangements();

// solution required