1.7 KiB
1.7 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4641000cf542c50ff76 | 問題 247: 双曲線の下にある正方形 | 5 | 301894 | problem-247-squares-under-a-hyperbola |
--description--
1 ≤ x, 0 ≤ y ≤ \frac{1}{x} の範囲にある領域について考えます。
S_1 を、曲線の下に収まる最大の正方形とします。
S_2 を、残りの領域に収まる最大の正方形とします。以降はこの繰り返しです。
S_n のインデックスを (左、下) の対で表します。「左」は S_n の左にある正方形の数、「下」は $S_n$の下にある正方形の数を示します。
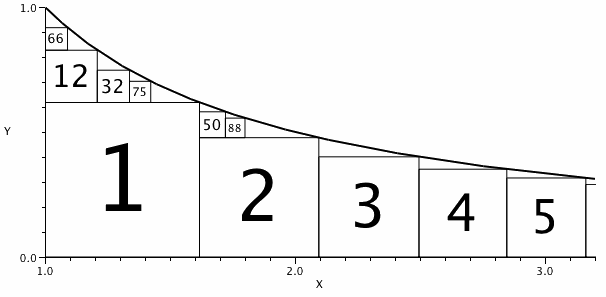
図では、配置した正方形に番号を付けてあります。
S_2 について見ると、正方形が左に 1 つあり、下にはないので、S_2 のインデックスは (1, 0) です。
S_{32} と S_{50} のインデックスがいずれも (1,1) であることが分かります。
S_n のインデックスが (1, 1) であるような最大の n は 50 です。
n のインデックスが (3, 3) であるような最大の S_n を求めなさい。
--hints--
squaresUnderAHyperbola() は 782252 を返す必要があります。
assert.strictEqual(squaresUnderAHyperbola(), 782252);
--seed--
--seed-contents--
function squaresUnderAHyperbola() {
return true;
}
squaresUnderAHyperbola();
--solutions--
// solution required