1.8 KiB
1.8 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4931000cf542c50ffa6 | 問題 295: レンズ状の穴 | 5 | 301947 | problem-295-lenticular-holes |
--description--
2 つの円に囲まれた凸状の領域が次の条件を満たす場合、その領域を「レンズ状の穴」と呼びます。
- 両方の円心が格子点上にある。
- 2 つの円が 2 つの相異なる格子点で交差する
- 両方の円に囲まれた凸状の領域が格子点を内包しない。
次のような円を考えます。
$$\begin{align} & C_0: x^2 + y^2 = 25 \\ & C_1: {(x + 4)}^2 + {(y - 4)}^2 = 1 \\ & C_2: {(x - 12)}^2 + {(y - 4)}^2 = 65 \end{align}$$
円 C_0, C_1, C_2 を下図に示します。
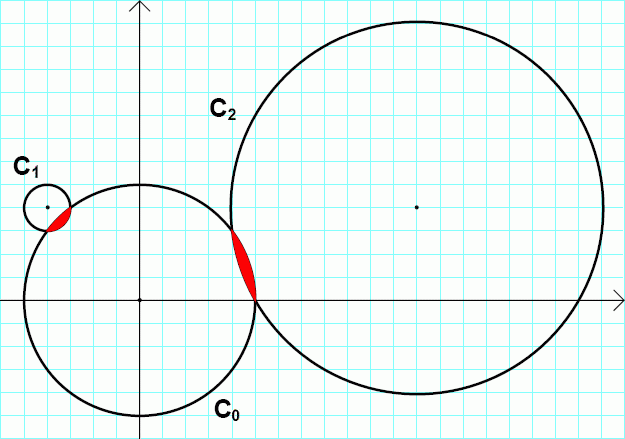
C_0 と C_1 はレンズ状の穴を形成し、C_0 と C_2 も同様です。
レンズ状の穴を形成する半径 r_1, r_2 の 2 つの円が存在する場合、正の実数の順序対 (r_1, r_2) を「レンズペア」と呼びます。 上の例では、(1, 5) と (5, \sqrt{65}) が共にレンズペアであることを確認できます。
0 < r_1 ≤ r_2 ≤ N となるような相異なるレンズペア (r_1, r_2) の個数を L(N) とします。 L(10) = 30, L(100) = 3442 であることを確認できます。
L(100\\,000) を求めなさい。
--hints--
lenticularHoles() は 4884650818 を返す必要があります。
assert.strictEqual(lenticularHoles(), 4884650818);
--seed--
--seed-contents--
function lenticularHoles() {
return true;
}
lenticularHoles();
--solutions--
// solution required